题目内容
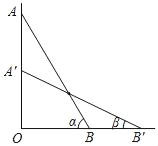
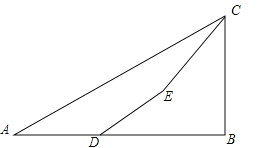
【题目】如图，为了测量某建筑物BC的高度，小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°，然后在水平地面上向建筑物前进了10m到达D处，此时遇到一斜坡，坡度i=1：
，沿着斜坡前进10米到达E处测得建筑物顶部的仰角是45°，请求出该建筑物BC的高度为（ ）（结果可带根号）
A. 5+5 B. 5
+5 C. 5+10 D. 5+10
【答案】D
【解析】
过E作EF⊥AB于F，EG⊥BC与G，根据矩形的性质得到四边形EG=FB，EF=BG，设CG=x，根据已知条件得到∠EDF=30°及直角三角形得到DF=10cos30°=5
，BG=EF=10sin30°=5，AB=10+5+x，BC=x+5．在Rt△ABC中，根据三角函数的定义列方程即可得到结论．
过E作EF⊥AB于F，EG⊥BC与G．
∵CB⊥AB，∴四边形EFBG是矩形，∴EG=FB，EF=BG，设CG=x米．
∵∠CEG=45°，∴FB=EG=CG=x．
∵DE的坡度i=1：，∴∠EDF=30°．
∵DE=10，∴DF=10cos30°=5，BG=EF=10sin30°=5，∴AB=10+5+x，BC=x+5．在Rt△ABC中，∵∠A=30°，∴BC=ABtan∠A，即x+5=
（10+5+x），解得：x=5+5，∴BC=5+5+5=（5+10）米．
故选D．
练习册系列答案
相关题目
