��Ŀ����
����Ŀ����֪����ABCD��һ����AD=8��E��BC���ϵ�һ�㣬������ABCD���ۺ�AE�۵���ʹ�ö���B����CD���ϵĵ�P����PC=4����ͼ1����
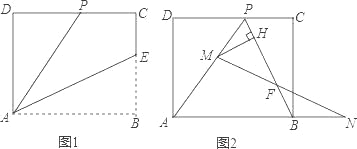
��1����AB�ij���
��2����ȥ�ۺ�AE������PB����M���߶�PA��һ�����㣨��M���P��A���غϣ���N��AB�س����ϵ�һ�����㣬��������PM=BN������M��MH��PB������ΪH������MN��PB�ڵ�F����ͼ2����
����M��PA���е㣬��MH�ij���
�����ʵ���M��N���ƶ������У��߶�FH�ij����Ƿ����仯�����仯��˵�����ɣ������䣬����߶�FH�ij��ȣ�
���𰸡�(1)10����2��![]() ��
�� ![]() .
.
�������������������1����AB=x�������۵��ɵ�AP=CD=x��DP=CD-CP=x-4�����ù��ɶ�������Rt��ADP�У�AD2+DP2=AP2����82+��x-4��2=x2�����ɽ��
��2��������A��AG��PB�ڵ�G�����ݹ��ɶ������PB�ij�����AP=AB������PG=BG=![]() PB=
PB=![]() ����Rt��AGP��AG=
����Rt��AGP��AG=![]() ��
��
��AG��PB��MH��PB������MH��AG������M��PA���е㣬����H��PG���е㣬������λ�ߵ����ʵõ�MH=![]() AG=
AG=![]() ��
��
����MQ��AN����PB�ڵ�Q�����MP=MQ��BN=QM���ó�MP=MQ������MH��PQ���ó�HQ=![]() PQ��������QMF=��BNF��֤����MFQ�ա�NFB���ó�QF=
PQ��������QMF=��BNF��֤����MFQ�ա�NFB���ó�QF=![]() QB�������EF=
QB�������EF=![]() PB��������HF=
PB��������HF=![]() PB���ɵó��߶�EF�ij��Ȳ��䣮
PB���ɵó��߶�EF�ij��Ȳ��䣮
�����������1����AB=x����AP=CD=x��DP=CD-CP=x-4��
��Rt��ADP��AD2+DP2=AP2��
��82+��x-4��2=x2��
��ã�x=10��
��AB=10��
��2������ͼ2������A��AG��PB�ڵ�G��
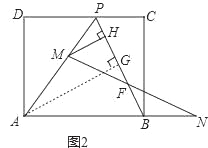
�ɣ�1���еĽ��ۿɵã�PC=4��BC=8����C=90����
��PB=![]() ��
��
��AP=AB��
��PG=BG=![]() PB=
PB=![]() ��
��
��Rt��AGP��AG=![]() ��
��
��AG��PB��MH��PB��
��MH��AG��
��M��PA���е㣬
��H��PG���е㣬
��MH=![]() AG=
AG=![]() ��
��
������M��N���ƶ������У��߶�FH�ij����Dz������仯��
��MQ��AN����PB�ڵ�Q����ͼ3��
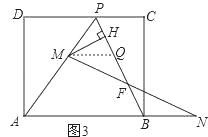
��AP=AB��MQ��AN��
���APB=��ABP=��MQP��
��MP=MQ��
��BN=PM��
��BN=QM��
��MP=MQ��MH��PQ��
��EQ=![]() PQ��
PQ��
��MQ��AN��
���QMF=��BNF��
����MFQ����NFB��
 ��
��
���MFQ�ա�NFB��AAS����
��QF=![]() QB��
QB��
��HF=HQ+QF=![]() PQ+
PQ+![]() QB=
QB=![]() PB=
PB=![]() ��
��
������M��N���ƶ������У��߶�FH�ij����Dz������仯������Ϊ![]() ��
��

 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д� �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�