题目内容
【题目】如图,AB∥CD,∠BAC与∠ACD的角平分线交于点E,且AC=13,AE=5,则AB与CD之间的距离是( )

A.7B.8C.![]() D.9
D.9
【答案】C
【解析】
作辅助线,构建垂线,根据角平分线上的点到角的两边的距离相等可得EG=EF=EH,再根据平行线间的距离的定义解答即可
解:过点E作EF⊥AC于点F,
作EG⊥AB于点G,交CD于点H。
∵AB∥CD
∴EH⊥CD
∵AE是∠BAC角平分线
∴EG=EF
∵CE是∠ACD的角平分线
∴EF=EH
∴GH=EG+EH=2EF
∵∠BAC与∠ACD的角平分线交于点E
∴∠CAE=![]() ∠BAC,∠ACE=
∠BAC,∠ACE=![]() ∠ACD
∠ACD
∵AB∥CD
∴∠BAC+∠ACD=180°
∴∠CAE+∠ACE=![]() ∠BAC+
∠BAC+![]() ∠ACD=90°
∠ACD=90°
∴△ACE是RT△
∴S△ACE=![]() AE×CE=
AE×CE=![]() AC×EF
AC×EF
∴EF=![]() .
.
由勾股定理得AC2=AE2+CE2
∴CE2=132-52=144
∴CE=12
∴EF=![]() =
=![]()
∴GH=![]()
∴AB与CD之间的距离为![]() .
.
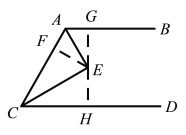
故选C

练习册系列答案
相关题目