题目内容
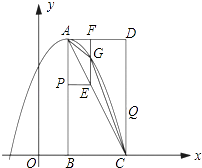
【题目】抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C,已知抛物线的对称轴为x=1,B(3,0),C(0,﹣3),
(1)求二次函数y=ax2+bx+c的解析式;
(2)在抛物线对称轴上是否存在一点P,使点P到B、C两点距离之差最大?若存在,求出P点坐标;若不存在,请说明理由;
(3)平行于x轴的一条直线交抛物线于M、N两点,若以MN为直径的圆恰好与x轴相切,求此圆的半径.
【答案】
(1)解:将C(0,﹣3)代入y=ax2+bx+c,
得c=﹣3.
将c=﹣3,B(3,0)代入y=ax2+bx+c,
得9a+3b+c=0.(1)
∵直线x=1是对称轴,
∴ ![]() .(2)(2分)
.(2)(2分)
将(2)代入(1)得
a=1,b=﹣2.
所以,二次函数得解析式是y=x2﹣2x﹣3.
(2)解:AC与对称轴的交点P即为到B、C的距离之差最大的点.
∵C点的坐标为(0,﹣3),A点的坐标为(﹣1,0),
∴直线AC的解析式是y=﹣3x﹣3,
又∵直线x=1是对称轴,
∴点P的坐标(1,﹣6).
(3)解:设M(x1,y)、N(x2,y),所求圆的半径为r, 
则x2﹣x1=2r,(1)
∵对称轴为直线x=1,即 ![]() =1,
=1,
∴x2+x1=2.(2)
由(1)、(2)得:x2=r+1.(3)
将N(r+1,y)代入解析式y=x2﹣2x﹣3,
得y=(r+1)2﹣2(r+1)﹣3.
整理得:y=r2﹣4.
由所求圆与x轴相切,得到r=|y|,即r=±y,
当y>0时,r2﹣r﹣4=0,
解得, ![]() ,
, ![]() (舍去),
(舍去),
当y<0时,r2+r﹣4=0,
解得, ![]() ,
, ![]() (舍去).
(舍去).
所以圆的半径是 ![]() 或
或 ![]() .
.
【解析】先利用待定系数法求出二次函数的解析式,然后再画出函数图象进行计算.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】“六一”前夕,某玩具经销商用去2350元购进A,B,C三种新型的电动玩具共50套,并且购进的三种玩具都不少于10套,设购进A种玩具x套,B种玩具y套,三种电动玩具的进价和售价如表所示
型 号 | A | B | C |
进价(元/套) | 40 | 55 | 50 |
售价(元/套) | 50 | 80 | 65 |
(1)用含x、y的代数式表示购进C种玩具的套数;
(2)求y与x之间的函数关系式;
(3)假设所购进的这三种玩具能全部卖出,且在购销这种玩具的过程中需要另外支出各种费用200元.
①求出利润P(元)与x(套)之间的函数关系式;②求出利润的最大值,并写出此时三种玩具各多少套.