ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНЉx2Љ2x+cЕФОЙ§DЃЈЉ2ЃЌ3ЃЉЃЌгыxжсНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЁЂгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНКЭAЁЂBСНЕузјБъЃЛ
ЃЈ2ЃЉдкХзЮяЯпЕФЖдГЦжсЩЯгавЛЕуPЃЌЪЙЕУЁЯOAPЃНЁЯBCOЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЕуMдкХзЮяЯпЩЯЃЌЕуNдкХзЮяЯпЖдГЦжсЩЯЃЎ
ЂйЕБЁЯACMЃН90ЁуЪБЃЌЧѓЕуMЕФзјБъЃЛ
ЂкЪЧЗёДцдкетбљЕФЕуMгыЕуNЃЌЪЙвдMЁЂNЁЂAЁЂCЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыжБНгаДГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
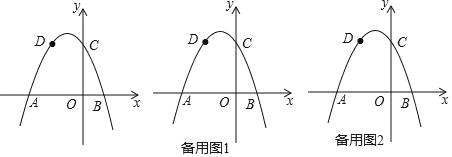
ЁОД№АИЁПЃЈ1ЃЉyЃНЉx2Љ2x+3ЃЌAЃЈЉ3ЃЌ0ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЈ2ЃЉP1ЃЈЉ1ЃЌ![]() ЃЉЃЛP2ЃЈЉ1ЃЌЉ
ЃЉЃЛP2ЃЈЉ1ЃЌЉ![]() ЃЉЃЈ3ЃЉM1ЃЈЉ2ЃЌ3ЃЉЃЌM2ЃЈЉ4ЃЌЉ5ЃЉЃЌM3ЃЈ2ЃЌЉ5ЃЉ
ЃЉЃЈ3ЃЉM1ЃЈЉ2ЃЌ3ЃЉЃЌM2ЃЈЉ4ЃЌЉ5ЃЉЃЌM3ЃЈ2ЃЌЉ5ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉНЋЕуDДњШыКЏЪ§НтЮіЪНЧѓГіc,НјЖјБэЪОГіЖўДЮКЏЪ§ЕФвЛАуЪНЃКyЃНЉx2Љ2x+3ЃЌСюy=0МДПЩЧѓГіA,BЕФзјБъЃЛ
ЃЈ2ЃЉЧѓГіЖўДЮКЏЪ§ЕФЖдГЦжс,НјЖјЧѓГіAH=2, CЃЈ0ЃЌ3ЃЉЃЌЕБЕуPдкxжсЕФЩЯЗНЪБЃЌЩшХзЮяЯпЕФЖдГЦжсгыxжсНЛгкЕуHЃЌвзжЄЁїAHPЁзЁїCOBЃЌЕУ![]() ЃЌМДПЩЧѓГіЕуP1ЃЈЉ1ЃЌ
ЃЌМДПЩЧѓГіЕуP1ЃЈЉ1ЃЌ![]() ЃЉЃЛЕБЕуPдкxжсЕФЯТЗНЪБЃЌМДгыЕуP1ЙигкxжсЖдГЦЪБЃЌЕуP2ЃЈЉ1ЃЌЉ
ЃЉЃЛЕБЕуPдкxжсЕФЯТЗНЪБЃЌМДгыЕуP1ЙигкxжсЖдГЦЪБЃЌЕуP2ЃЈЉ1ЃЌЉ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉЂйЙ§ЕуMзїMIЁЭyжсЃЌДЙзуЮЊIЃЌгЩЃЈ2ЃЉжЊЃКAOЃНCOЃЌдђЁЯACOЃНЁЯCAOЃН45ЁуЃЌРћгУЕШбќжБНЧШ§НЧаЮаджЪЕУMIЃНCIЃЌЩшMЃЈxЃЌЉx+3ЃЉЃЌевЕНЕШСПЙиЯЕЉx2Љ2x+3ЃНЉx+3ЃЌМДПЩЧѓГіMЃЈЉ1ЃЌ4ЃЉЃЛЂкЩшГіM,NЕФзјБъ,ЗжБ№ЧѓГіЖдНЧЯпЕФжаЕу,РћгУЦНааЫФБпаЮЕФЖдНЧЯпЛЅЯрЦНЗжетвЛаджЪНЈСЂЗНГЬзщ,ЧѓНтМДПЩ,МћЯъНт.
ЃЈ1ЃЉЁпХзЮяЯпyЃНЉx2Љ2x+cЕФОЙ§DЃЈЉ2ЃЌ3ЃЉЃЌ
ЁрЉ4+4+cЃН3ЃЌ
НтЕУЃКcЃН3ЃЌ
МДХзЮяЯпЕФБэДяЪНЮЊЃКyЃНЉx2Љ2x+3ЃЌ
ЩшyЃН0ЃЌдђ0ЃНЉx2Љ2x+3ЃЌ
НтЕУЃКx1ЃНЉ3ЃЌx2ЃН1ЃЌ
ЁпЕуAдкЕуBЕФзѓВрЃЌ
ЁрAЃЈЉ3ЃЌ0ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЛ
ЃЈ2ЃЉЁпyЃНЉx2Љ2x+3ЃНЉЃЈx+1ЃЉ2+4ЃЌ
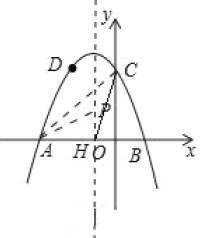
ЁрХзЮяЯпЕФЖдГЦжсЮЊжБЯпxЃНЉ1ЃЌСюХзЮяЯпЖдГЦжсКЭxжсНЛгкЕуH,
ЁрAHЃН2ЃЌСюxЃН0ЃЌдђyЃНЉx2Љ2x+3ЃН3ЃЌ
МДЕуCЃЈ0ЃЌ3ЃЉЃЌ
ЕБЕуPдкxжсЕФЩЯЗНЪБЃЌЩшХзЮяЯпЕФЖдГЦжсlгыxжсНЛгкЕуHЃЌ
ЁпЁЯOAPЃНЁЯBCOЃЌЁЯAHPЃНЁЯCOBЃН90ЁуЃЌ
ЁрЁїAHPЁзЁїCOBЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
НтЕУЃКPHЃН![]() ЃЌ
ЃЌ
ЁрЕуP1ЃЈЉ1ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЕБЕуPдкxжсЕФЯТЗНЪБЃЌМДгыЕуP1ЙигкxжсЖдГЦЪБЃЌЕуP2ЃЈЉ1ЃЌЉ![]() ЃЉЃЛ
ЃЉЃЛ
злЩЯЫљЪіЃКЕуPЕФзјБъЮЊЃКP1ЃЈЉ1ЃЌ![]() ЃЉЃЛP2ЃЈЉ1ЃЌЉ
ЃЉЃЛP2ЃЈЉ1ЃЌЉ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉЂйЙ§ЕуMзїMIЁЭyжсЃЌДЙзуЮЊIЃЌгЩЃЈ2ЃЉжЊЃКAOЃНCOЃЌдђЁЯACOЃНЁЯCAOЃН45ЁуЃЌ
ЁпЁЯACMЃН90ЁуЃЌ
ЁрЁЯMCIЃН45ЁуЃЌ
ЁрMIЃНCIЃЌЩшMЃЈxЃЌЉx+3ЃЉЃЌ
ЁрЉx2Љ2x+3ЃНЉx+3ЃЌ
НтЕУЃКx1ЃНЉ1ЃЌx2ЃН0ЃЈЩсШЅЃЉЃЌ
МДMЃЈЉ1ЃЌ4ЃЉЃЛ
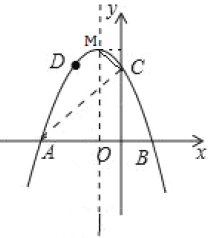
ЂкМйЩшДцдкТњзуЬтвтЕФM,N,ЩшMЃЈm,-m2-2m+3ЃЉ,N(-1,n)гЩЃЈ1ЃЉЃЈ2ЃЉЮЪПЩжЊA(-3,0)C(0,3),
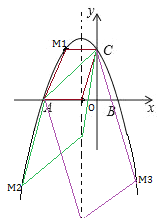
ШєACЮЊЦНааЫФБпаЮЖдНЧЯп,
ЁпЯпЖЮACЕФжаЕузјБъЮЊЃЈ![]() ,
,![]() ЃЉ,ЯпЖЮMNЕФжаЕузјБъЮЊЃЈ
ЃЉ,ЯпЖЮMNЕФжаЕузјБъЮЊЃЈ![]() ЃЉ,
ЃЉ,
Ёр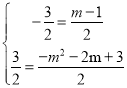
НтЕУЃКm=-2,n=0,дђ-m2-2m+3=3,МДЕуMЕФзјБъЮЊM1ЃЈЉ2ЃЌ3ЃЉЃЌ
ШєANЮЊЦНааЫФБпаЮЖдНЧЯп,ЭЌРэПЩЕУ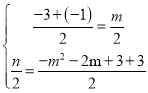
НтЕУЃКm=-4,n=-2,дђ-m2-2m+3=-5,МДЕуMЕФзјБъЮЊM2ЃЈЉ4ЃЌЉ5ЃЉЃЌ
ШєAMЮЊЦНааЫФБпаЮЖдНЧЯп,ЭЌРэПЩЕУ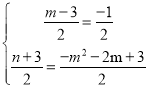
НтЕУЃКm=2,n=-8,дђ-m2-2m+3=-5,МДЕуMЕФзјБъЮЊM3ЃЈ2ЃЌЉ5ЃЉ
ЫљвдMгаШ§ЕуЃЌДЫMЕФзјБъЮЊM1ЃЈЉ2ЃЌ3ЃЉЃЌM2ЃЈЉ4ЃЌЉ5ЃЉЃЌM3ЃЈ2ЃЌЉ5ЃЉ

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ