题目内容
【题目】将两边长分别是
和
的矩形以其一边所在的直线为轴旋转一周，所得的几何体的侧面积是_____
.
【答案】
【解析】
根据长方形绕一边旋转一周，可得圆柱．分类讨论：将矩形以6cm的一边所在直线为轴旋转一周，那么圆柱的底面半径为4cm，高为6cm，那么圆柱的侧面积为底面圆周长乘以圆柱的高；若将矩形以4cm的一边所在直线为轴旋转一周，那么圆柱的底面半径为6cm，高为4cm，用同样方法即可求出圆柱体的侧面积．
解：这个长方形绕一边所在直线旋转一周后是圆柱．
当把矩形6cm的一边所在直线为轴旋转一周，那么圆柱的底面半径为4cm，高为6cm，
∴圆柱的侧面积为4×2π×6=48π（cm2）；
当把矩形4cm的一边所在直线为轴旋转一周，那么圆柱的底面半径为6cm，高为4cm，
∴圆柱的侧面积为6×2π×4=48π（cm2）.
故答案为：48π.
练习册系列答案
相关题目
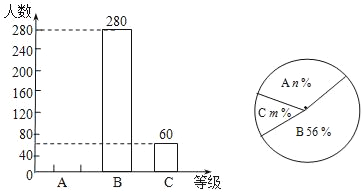
【题目】为了传承中华优秀传统文化，市教育局决定开展“经典诵读进校园”活动，某校团委组织八年级100名学生进行“经典诵读”选拔赛，赛后对全体参赛学生的成绩进行整理，得到下列不完整的统计图表。
组别 | 分数段 | 频次 | 频率 |
A | 60x<70 | 17 | 0.17 |
B | 70x<80 | 30 | a |
C | 80x<90 | b | 0.45 |
D | 90x<100 | 8 | 0.08 |
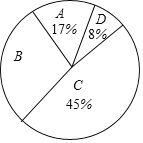
请根据所给信息，解答以下问题：
(1)表中a=___，b=___；
(2)请计算扇形统计图中B组对应扇形的圆心角的度数；
(3)已知有四名同学均取得98分的最好成绩，其中包括来自同一班级的甲、乙两名同学，学校将从这四名同学中随机选出两名参加市级比赛，请用列表法或画树状图法求甲、乙两名同学都被选中的概率。
