Question

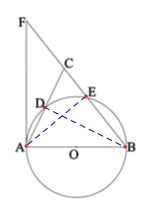
【题目】如图，在△ABC中，以AB为直径作圆交AC、BC于点D、E两点，AF切⊙O于点A，点D是AC中点．

（1）求证：AB=BC；

（2）若，CF=，求⊙O的半径．

Answer 1

【答案】（1）证明见解析；（2）半径为．

【解析】

（1）连接BD，易证BD⊥AC，结合点D是AC中点，即可得到结论；

（2）连接AE，设CE=，则AC=4k，CD=2k，由CAE~CBD，得，从而得BC=，BE=，由AEF~BEA，得，结合，得k=，进而即可求解．

（1）连接BD，

∵AB是⊙O的直径，

∴∠ADB=90°，即：BD⊥AC，

又∵点D是AC中点，

∴BD是AC的中垂线，

∴AB=BC；

（2）连接AE，

∵，

∴设CE=，则AC=4k，

∵点D是AC中点，

∴CD=AC=2k，

∵AB是⊙O的直径，

∴∠AEC=∠BDC=90°，

又∵∠CAE=∠CBD，

∴CAE~CBD，

∴，即：，

∴BC=，BE=-=，

∵AF切⊙O于点A，

∴AB⊥AF，

∴∠FAE+∠BAE=∠EAB+∠ABE=90°，

∴∠FAE=∠ABE，

∵∠AEF=∠BEA=90°，

∴AEF~BEA，

∴，即：，

又∵, CF=，

∴，解得：k=，

∴，BE==，

∴，

∴⊙O的半径为：．