��Ŀ����
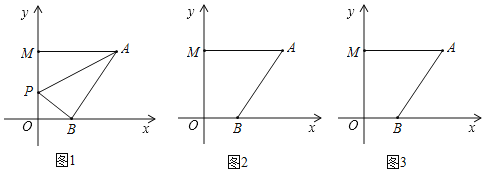
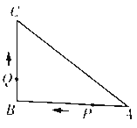
����Ŀ����ͼ����֪��ABC�У���B=90�㣬AB=8 cm��BC=6 cm��P��Q�ǡ�ABC���ϵ��������㣬��P�ӵ�A��ʼ��A��B�����˶������ٶ�Ϊ1 cm����Q�ӵ�B��ʼ��B��C�����˶������ٶ�Ϊ2 cm/s������ͬʱ���������˶���ʱ��Ϊt s.
��1���˶�����ʱ����APC�ǵ��������Σ�
��2������Q�ڱ�CA���˶�ʱ������ʹ��BCQ��Ϊ���������ε��˶�ʱ��.
���𰸡���1���˶�![]() sʱ����APC�ǵ���������.��2�����˶�ʱ��Ϊ5.5 s ��6 s ��6.6 sʱ����BCQΪ����������.
sʱ����APC�ǵ���������.��2�����˶�ʱ��Ϊ5.5 s ��6 s ��6.6 sʱ����BCQΪ����������.
��������
��1����������ã�AP=PC���з��̣���⼴�ɣ�
��2����BQ=BC��CQ=BC��BQ=CQ��������ֱ����۵õ�����t�ķ��̣����t���ɣ�
��1���������֪AP=t��PC=![]()
��AP=PC��
��t=![]() ��
��
��ã�t=![]() ��
��
�����![]() �����APC���γɵ��������Σ�
�����APC���γɵ��������Σ�
��2������ABC�У��ɹ��ɶ��������AC=10��
����Q��AC��ʱ��AQ=BC+AC-2t=16-2t������CQ=AC-AQ=10-��16-2t��=2t-6��
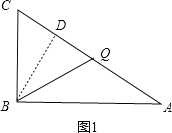
��BQ=BC=6ʱ����ͼ1����B��BD��AC����CD=![]() CQ=t-3����Rt��ABC�У������BD=
CQ=t-3����Rt��ABC�������BD=![]() ��
��
��Rt��BCD�У��ɹ��ɶ����ɵ�BC2=BD2+CD2����62=��![]() ��2+��t-3��2��
��2+��t-3��2��
���t=![]() ��t=-
��t=-![]() ��0����ȥ����
��0����ȥ����
��CQ=BC=6ʱ����2t-6=6�����t=6��
��CQ=BQʱ�����C=��QBC��
���C+��A=��CBQ+��QBA��
���A=��QBA��
��QB=QA��
��CQ=![]() AC=5����2t-6=5�����t=5.5��
AC=5����2t-6=5�����t=5.5��
���Ͽ�֪����BCQΪ����������ʱ��t=![]() ��t=6��t=5.5��
��t=6��t=5.5��

 ��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д�
��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д� Сѧ��ĩ���Ծ�ϵ�д�
Сѧ��ĩ���Ծ�ϵ�д�