Question

【题目】某商店第一次用600元购进2B铅笔若干支，第二次又用600元购进该款铅笔，但这次每支的进价是第一次进价的倍，购进数量比第一次少了30支．

（1）求第一次每支铅笔的进价是多少元？

（2）若要求这两次购进的铅笔按同一价格全部销售完毕后获利不低于420元，问每支售价至少是多少元？

Answer 1

【答案】解：（1）设第一次每支铅笔进价为x元，由第二次每支铅笔进价为x元。

根据题意列方程得，，解得，x=4。

检验：当x=4时，分母不为0，

∴x=4是原分式方程的解。

答：第一次每支铅笔的进价为4元。

（2）设售价为y元，根据题意列不等式为：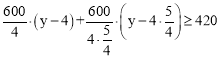

解得，y≥6。

答：每支售价至少是6元。

【解析】分式方程和一元一次不等式组的应用。

（1）方程的应用解题关键是找出等量关系，列出方程求解。设第一次每支铅笔进价为x元，由第二次每支铅笔进价为x元。本题等量关系为：

第一次购进数量－第二次购进数量=30

－ =30。

（2）设售价为y元，求出利润表达式，然后列不等式解答。利润表达式为：

第一次购进数量×第一次每支铅笔的利润＋第二次购进数量×第二次每支铅笔的利润

· ＋ · 。