题目内容
 (2013•南安市质检)一个正方体物体沿斜坡向上滑动,其截面如图所示,正方形DEFH的边长为1米,坡角∠A=30°,∠B=90°,BC=3米,则:
(2013•南安市质检)一个正方体物体沿斜坡向上滑动,其截面如图所示,正方形DEFH的边长为1米,坡角∠A=30°,∠B=90°,BC=3米,则:(1)AC的长是
6
6
米;(2)当正方体DEFH运动到什么位置,即当AE=
| 7 |
| 3 |
| 7 |
| 3 |
分析:(1)根据坡角和BC的长求得AC的长即可;
(2)根据已知得出假设AE=x,可得EC=6-x,利用勾股定理得出DC2=DE2+EC2=1+(6-x)2,AE2+BC2=x2+9,即可求出x的值.
(2)根据已知得出假设AE=x,可得EC=6-x,利用勾股定理得出DC2=DE2+EC2=1+(6-x)2,AE2+BC2=x2+9,即可求出x的值.
解答: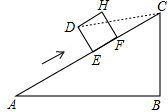 解:(1)∵坡角∠A=30°,∠B=90°,BC=3米,
解:(1)∵坡角∠A=30°,∠B=90°,BC=3米,
∴AC=2BC=6米;
(2)如图,连接CD,
假设AE=x,可得EC=6-x,
∵坡角∠A=30°,∠B=90°,BC=3米,
∴AC=6米,
∵正方形DEFH的边长为1米,即DE=1米,
∴DC2=DE2+EC2=1+(6-x)2,
AE2+BC2=x2+9,
∵DC2=AE2+BC2,
∴1+(6-x)2=x2+9,
解得:x=
米.
故答案为:6,
.
 解:(1)∵坡角∠A=30°,∠B=90°,BC=3米,
解:(1)∵坡角∠A=30°,∠B=90°,BC=3米,∴AC=2BC=6米;
(2)如图,连接CD,
假设AE=x,可得EC=6-x,
∵坡角∠A=30°,∠B=90°,BC=3米,
∴AC=6米,
∵正方形DEFH的边长为1米,即DE=1米,
∴DC2=DE2+EC2=1+(6-x)2,
AE2+BC2=x2+9,
∵DC2=AE2+BC2,
∴1+(6-x)2=x2+9,
解得:x=
| 7 |
| 3 |
故答案为:6,
| 7 |
| 3 |
点评:此题主要考查了坡度坡角问题、勾股定理的应用以及一元二次方程的应用,根据已知表示出CE,AE的长度是解决问题的关键.

练习册系列答案
相关题目
 (2013•南安市质检)如图,∠AOB的两边OA、OB均为平面反光镜,∠AOB=40°,从OB上一点E射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行,则∠DEB的度数是( )
(2013•南安市质检)如图,∠AOB的两边OA、OB均为平面反光镜,∠AOB=40°,从OB上一点E射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行,则∠DEB的度数是( )
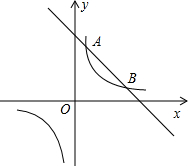 (2013•南安市质检)如图,已知点A(1,a)和点B(3,b)是直线y=mx+n与双曲线
(2013•南安市质检)如图,已知点A(1,a)和点B(3,b)是直线y=mx+n与双曲线