题目内容
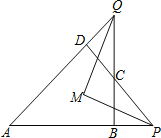
【题目】如图,已知四边形ABCD中,∠A+∠DCB=180°,两组对边延长后,分别交于P、Q两点,∠APD、∠AQB的平分线交于M,求证:PM⊥QM.
【答案】证明见解析
【解析】
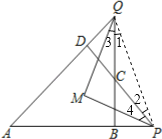
试题分析:连接PQ,由三角形内角和定理可得出∠QCP=180°﹣∠1﹣∠2,∠A=180°﹣∠AQP﹣∠APQ=180°﹣∠1﹣∠2﹣∠AQB﹣∠APD,再根据∠APD、∠AQB的平分线交于点M可知∠AQB=2∠3,∠APD=2∠4,再由三角形外角的性质可得出∠QMP=![]() (∠BCD+∠A),进而得出结论.
(∠BCD+∠A),进而得出结论.
证明:连接PQ,
∵∠QCP=180°﹣∠1﹣∠2,
∠A=180°﹣∠AQP﹣∠APQ=180°﹣∠1﹣∠2﹣∠AQB﹣∠APD,
又∵∠APD、∠AQB的平分线交于点M,
∴∠AQB=2∠3,∠APD=2∠4,
∴∠QCP+∠A=(180°﹣∠1﹣∠2)+(180°﹣∠1﹣∠2﹣2∠3﹣2∠4)
=360°﹣2∠1﹣2∠2﹣2∠3﹣2∠4,
∴![]() (∠QCP+∠A)=180°﹣∠1﹣∠2﹣∠3﹣∠4,
(∠QCP+∠A)=180°﹣∠1﹣∠2﹣∠3﹣∠4,
又∵∠BCD=∠QCP,
∴![]() (∠BCD+∠A)=180°﹣∠1﹣∠2﹣∠3﹣∠4,
(∠BCD+∠A)=180°﹣∠1﹣∠2﹣∠3﹣∠4,
又∵∠QMP=180°﹣∠MQP﹣∠MPQ=180°﹣∠1﹣∠3﹣∠2﹣∠4,
∴∠QMP=![]() (∠BCD+∠A)=
(∠BCD+∠A)=![]() ×180°=90°,即PM⊥QM.
×180°=90°,即PM⊥QM.

练习册系列答案
相关题目