题目内容
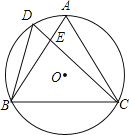
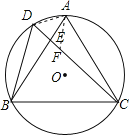
【题目】如图,D是正△ABC的外接圆⊙O上弧AB上一点,给出下列结论:①∠BDC=∠ADC=60°;②AEBE=CEED;③CA2=CECD;④CD=BD+AD.其中正确的个数是( )
A.4 B.3 C.2 D.1
【答案】A
【解析】
试题分析:连接AD,根据等边三角形的性质得到∠BAC=∠ABC=60°,由圆周角定理得到∠BDC=∠BAC=60°,∠ADC=∠ABC=60°,于是得到∠BDC=∠ADC=60°,故①正确;根据圆周角定理得到∠D=∠A,∠ABD=∠ACD,推出△BDE∽△ACE,根据相似三角形的性质即可得到AEBE=CEED;故②正确;由于∠ADC=∠EAC=60°,∠ACE=∠ACD,得到△ACD∽△ACE,根据相似三角形的性质得到CA2=CECD;故③正确;在CD上截取CF=BD,通过△ABD≌△ACF,得到AD=AF,推出△ADF是等边三角形,得到DF=AD,等量代换即可得到结论.
解:连接AD,∵△ABC是等边三角形,
∴∠BAC=∠ABC=60°,
∴∠BDC=∠BAC=60°,∠ADC=∠ABC=60°,
∴∠BDC=∠ADC=60°,故①正确;
∵∠D=∠A,∠ABD=∠ACD,
∴△BDE∽△ACE,
∴![]() ,
,
∴AEBE=CEED;故②正确;
∵∠ADC=∠EAC=60°,∠ACE=∠ACD,
∴△ACD∽△ACE,
∴![]() ,
,
∴CA2=CECD;故③正确;
在CD上截取CF=BD,
在△ABD与△ACF中,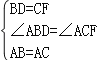 ,
,
∴△ABD≌△ACF,
∴AD=AF,
∵∠ADC=60°,
∴△ADF是等边三角形,
∴DF=AD,
∵CD=CF+DF,
∴CD=BD+AD.故④正确.
故选A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目