题目内容
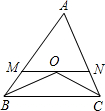 如图,OB平分∠CBA,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=18,则△AMN的周长为
如图,OB平分∠CBA,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=18,则△AMN的周长为
- A.30
- B.33
- C.36
- D.39
A
分析:根据BO平分∠CBA,CO平分∠ACB,且MN∥BC,可得出MO=MC,NO=NB,所以三角形AMN的周长是AB+AC.
解答:∵BO平分∠CBA,CO平分∠ACB,
∴∠NBO=∠OBC,∠OCM=∠OCB,
∵MN∥BC,
∴∠NOB=∠OBC,∠MOC=∠OCB,
∴∠NBO=∠NOB,∠MOC=∠MCO,
∴MO=MC,NO=NB,
∵AB=12,AC=18,
∴△AMN的周长=AM+MN+AN=AB+AC=12+18=30.
故选A.
点评:本题主要考查学生对考查了等腰三角形的判定和性质以及平行线的性质等知识点的理解和掌握,难度不大,是基础知识要熟练掌握.
分析:根据BO平分∠CBA,CO平分∠ACB,且MN∥BC,可得出MO=MC,NO=NB,所以三角形AMN的周长是AB+AC.
解答:∵BO平分∠CBA,CO平分∠ACB,
∴∠NBO=∠OBC,∠OCM=∠OCB,
∵MN∥BC,
∴∠NOB=∠OBC,∠MOC=∠OCB,
∴∠NBO=∠NOB,∠MOC=∠MCO,
∴MO=MC,NO=NB,
∵AB=12,AC=18,
∴△AMN的周长=AM+MN+AN=AB+AC=12+18=30.
故选A.
点评:本题主要考查学生对考查了等腰三角形的判定和性质以及平行线的性质等知识点的理解和掌握,难度不大,是基础知识要熟练掌握.

练习册系列答案
相关题目
 如图,A是∠MON边OM上一点,AE∥ON.
如图,A是∠MON边OM上一点,AE∥ON.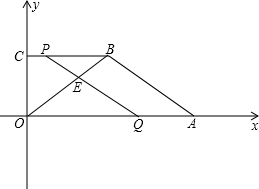 2个单位/秒的速度向点O 移动.设点P、Q同时出发,运动的时间为t(秒)
2个单位/秒的速度向点O 移动.设点P、Q同时出发,运动的时间为t(秒)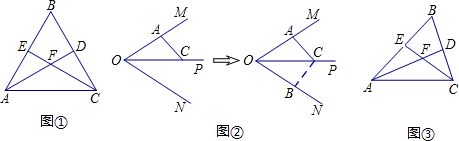
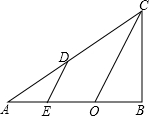 如图,在Rt△ABC,∠ABC=90°,CO平分∠ACB交于AB于O,D为AC上一点,且CD=CB,E为AO上一点,OE=OB,连接DE
如图,在Rt△ABC,∠ABC=90°,CO平分∠ACB交于AB于O,D为AC上一点,且CD=CB,E为AO上一点,OE=OB,连接DE