Question

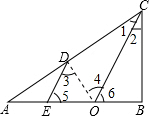
如图，在Rt△ABC，∠ABC=90°，CO平分∠ACB交于AB于O，D为AC上一点，且CD=CB，E为AO上一点，OE=OB，连接DE
①试判断直线DE与OC的位置关系，并证明你的结论
②若AD=4，CD=6，求AE的长．

Answer 1

分析：（1）DE∥OC．通过△CDO≌△CBO推知OD=OB，∠DOC=∠BCO；然后利用角平分线的性质以及等量代换证得内错角∠EDO=∠DOC；
（2）在直角△ABC中根据勾股定理求得AB=8；然后在直角△ADO中利用勾股定理来求AO的长度．

解答：解：（1）直线DE与OC相互平行．理由如下：
如图连接OD．
∵CO平分∠ACB，
∴∠1=∠2．
∵在△CDO与△CBO中，

CD=CB ∠1=∠2 CO=CO

，
∴△CDO≌△CBO（SAS），
∴OD=OB，∠4=∠6．
又∵OE=OB，
∴∠3=∠5．
∵∠4+∠6=180°-∠DOE=∠3+∠5，
∴2∠4=2∠3，即∠4=∠3，
∴DE∥OC，即直线DE与OC相互平行；

（2）∵AD=4，CD=6，
∴AC=10．
∵在Rt△ABC，∠ABC=90°，
∴根据勾股定理求得AB=

AC2-BC2

=8．
设AE=x．则OD=OE=

1

2

（AB-AE）=

8-x

2

．
在直角△ADO中，AD²+OD²=OA²，即4²+（

8-x

2

）²=（x+

8-x

2

）²，
解得x=2，即AE=2．

点评：本题考查了全等三角形的判定与性质、勾股定理．解答（2）题时，借助于方程求得线段AE的长度．