Question

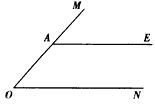
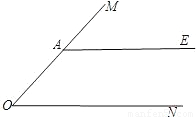
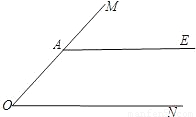
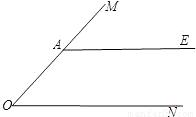
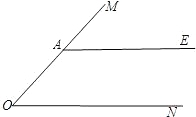如图，A是∠MON边OM上一点，AE∥ON．
（1）在图中作∠MON的角平分线OB，交AE于点B；（要求：尺规作图，保留作图痕迹，不写作法和证明）
（2）在（1）中，过点A画OB的垂线，垂足为点D，交ON于点C，连接CB，将图形补充完整，并证明四边形OABC是菱形．

Answer 1

分析：（1）角平分线的作法：用圆规以顶点为圆心，任意长为半径画一个弧（要保证有两个交点，不要太小），再以刚才画出的交点为顶点，以大于第一次的半径为半径画弧（左右各画一个弧），再取两道弧的交点，并连接这个交点的一开始最上面的顶点，这就是角平分线．
（2）本题可根据“一组邻边相等的平行四边形是菱形”，先证明OABC是个平行四边形，然后证明OA=AB即可．

解答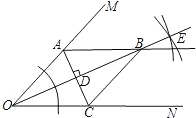：解：（1）如图，射线OB为所求作的图形．

（2）证明：∵OB平分∠MON，
∴∠AOB=∠BOC．
∵AE∥ON，
∴∠ABO=∠BOC．
∴∠AOB=∠ABO，AO=AB．
∵AD⊥OB，
∴BD=OD．
在△ADB和△CDO中
∵

∠ABD=∠COD BD=OD ∠ADB=∠CDO

∴△ADB≌△CDO，AB=OC．
∵AB∥OC，
∴四边形OABC是平行四边形．
∵AO=AB，
∴四边形OABC是菱形．

点评：本题考查尺规作图、全等三角形的判定，性质及特殊四边形的判定问题，解决本题的关键是熟悉基本作图，熟悉特殊平行四边形的判定方法．