题目内容
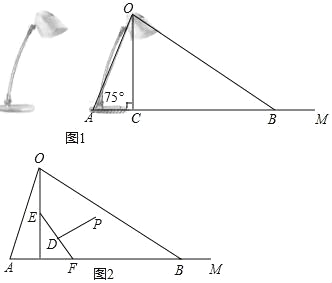
【题目】如图1为放置在水平桌面上的台灯的平面示意图,灯臂AO长为50cm,与水平桌面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平桌面所形成的夹角∠OCA,∠OBA分别为90°和30°.(不考虑其他因素,结果精确到0.1cm. sin75°≈0.97,cos75°≈0.26,![]() ≈1.73
≈1.73
(1)求该台灯照亮水平桌面的宽度BC.
(2)人在此台灯下看书,将其侧面抽象成如图2所示的几何图形,若书与水平桌面的夹角∠EFC为60°,书的长度EF为24cm,点P为眼睛所在位置,当点P在EF 的垂直平分线上,且到EF距离约为34cm(人的正确看书姿势是眼睛离书距离约1尺≈34cm)时,称点P为“最佳视点”.请通过计算说明最佳视点P在不在灯光照射范围内?
【答案】(1) 该台灯照亮水平面的宽度BC大约是83.9cm;(2) 最佳视点P在灯光照射范围内,理由见解析.
【解析】
试题分析:(1)在直角三角形ACO中,根据sin75°=![]() ,求出OC,在直角三角形BCO中,tan30°=
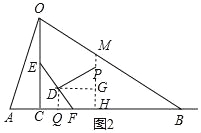
,求出OC,在直角三角形BCO中,tan30°=![]() ,求出BC即可.(2)如图,过点P作PH⊥AB于H,交OB于M,过点D作DG⊥PH于G,DQ⊥AB于Q,则四边形DGHQ为矩形,∠GDF=∠EFC=∠DPG=60°,求出PH,MH的长即可判断.
,求出BC即可.(2)如图,过点P作PH⊥AB于H,交OB于M,过点D作DG⊥PH于G,DQ⊥AB于Q,则四边形DGHQ为矩形,∠GDF=∠EFC=∠DPG=60°,求出PH,MH的长即可判断.
试题解析:(1)在直角三角形ACO中,sin75°=![]() ,
,
解得OC=50×0.97≈48.5,
在直角三角形BCO中,tan30°=![]() ,
,
解得BC=1.73×48.5≈83.9.
答:该台灯照亮水平面的宽度BC大约是83.9cm,
(2)如图,过点P作PH⊥AB于H,交OB于M,过点D作DG⊥PH于G,DQ⊥AB于Q,则四边形DGHQ为矩形,∠GDF=∠EFC=∠DPG=60°
由题意DE=DF=12,DP=34,
∴PG=17,QH=DG=17![]() ,QF=6,GH=DQ=6
,QF=6,GH=DQ=6![]() ,
,
∴PH=PH+GH=17+6![]() ≈27.38,
≈27.38,
又∵CH=6+17![]() ≈35.41
≈35.41
∴HB=CB﹣CH=83.9﹣35.41≈48.49,
∵∠OBC=30°,tan∠OBC=1:![]() ,
,
∴MH=HB÷![]() =48.49÷
=48.49÷![]() ≈28.03,
≈28.03,
∵27.38<28.03,
∴最佳视点P在灯光照射范围内.

【题目】某校初三学生开展踢毽子活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀.表是甲班和乙班成绩最好的5名学生的比赛成绩.
1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
甲班 | 100 | 98 | 102 | 97 | 103 | 500 |
乙班 | 99 | 100 | 95 | 109 | 97 | 500 |
经统计发现两班5名学生踢毽子的总个数相等.此时有学生建议,可以通过考查数据中的其它信息作为参考.请你回答下列问题:
(1)甲班的优秀率为60%,则乙班的优秀率为 ;
(2)甲班比赛成绩的方差S甲2=![]() ,求乙班比赛成绩的方差;
,求乙班比赛成绩的方差;
(3)根据以上信息,你认为应该把团体第一名的奖状给哪一个班?简述理由.