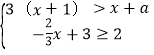题目内容
【题目】定义：如果M个不同的正整数，对其中的任意两个数，这两个数的积能被这两个数的和整除，则称这组数为M个数的自然数组，如（3，6）为两个数的自然数组，因为（3×6）能被（3+6）整除；又如（15，30，60）为三个数的自然数组，因为（15×30）能被（15+30）整除，（15×60）能被（15+60）整除，（30×60）能被（30+60）整除…
（1）求证：2n和n（n﹣2）（n≥3，n为整数）组成的数组是两个数的自然数组；
（2）若（4a，5a，6a）是三个数的自然数组，求满足条件的三位正整数a，并判断（4a+5，5a+5，6a+5）是否为自然数组．
【答案】（1）详见解析；（2）不是，理由详见解析.
【解析】
（1）根据祖冲之数组的定义，即可解决问题；（2）首先根据定义判断出a是5，9，11的公倍数，由此即可解决问题．
（1）∵2nn（n-2）=2n2（n-2），而2n+n（n-2）=n2
且：2n2（n-2）能被n2整除，
∴2n和n（n-2）（n≥3，n为整数）组成的数组是两个数的自然数组．
（2）∵(4a,5a,6a)是三个数的自然数组，
∴
，
，
都是整数，
∴a是5、9、11的公倍数，
∴5
911=495，4952=990，
∴满足条件的三位正整数a为495或990.
同理：当a=990时
不能整除，
故(4a+5,5a+5,6a+5)不是自然数组.
练习册系列答案
相关题目
