题目内容
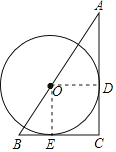
【题目】已知在Rt△ABC中,∠C=90°;以斜边AB上的一点O为圆心作圆O,与AC、BC分别相切与点D、E.
(1)求证:CD=CE;
(2)若AC=8,AB=10;求AD的长.
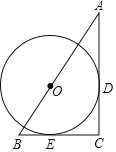
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD、OE,根据切线的性质、正方形的判定定理得到四边形OECD为正方形,根据正方形的性质证明结论;
(2)根据勾股定理求出BC,证明△AOD∽△ABC,根据相似三角形的性质列出比例式,计算即可.
(1)连接OD、OE,
∵AC、BC都与圆O相切,
∴OE⊥BC,OD⊥AC,又∠C=90°,
∴四边形OECD为矩形,
∵OD=OE,
∴四边形OECD为正方形,
∴CD=CE;
(2)设圆O的半径为r,
在Rt△ABC中,BC=![]()
∵OD⊥AC,∠C=90°,∠A=∠A,
∴△AOD∽△ABC,
∴![]() =即
=即![]()
解得,r=![]()
∴AD=AC﹣CD=8﹣![]() =
=![]()
故答案为:![]()

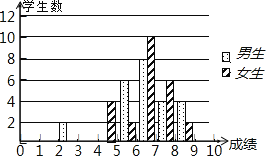
【题目】为了迎接体育中考,初三7班的体育老师对全班48名学生进行了一次体能模拟测试,得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分以上(包括9分)为优秀,这次模拟测试中男、女生全部成绩分布的条形统计图如下
(1)请补充完成下面的成绩统计分析表:
平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
男生 | 6.9 | 2.4 | ______ | 91.7% | 16.7% |
女生 | ______ | 1.3 | ______ | 83.3% | 8.3% |
(2)男生说他们的合格率、优秀率均高于女生,所以他们的成绩好于女生,但女生不同意男生的说法,认为女生的成绩要好于男生,请给出两条支持女生观点的理由;
(3)体育老师说,咱班的合格率基本达标,但优秀率太低,我们必须加强体育锻炼,两周后的目标是:全班优秀率达到50%.如果女生新增优秀人数恰好是男生新增优秀人数的两倍,那么男、女生分别新增多少优秀人数才能达到老师的目标?