题目内容
【题目】为判断命题“有三条边相等且一组对角相等的四边形是菱形”的真假,数学课上,老师给出菱形ABCD如图1,并作出了一个四边形ABC′D.具体作图过程如下:
如图2,在菱形ABCD中,
①连接BD,以点B为圆心,以BD的长为半径作圆弧,交CD于点P;
②分别以B、D为圆心,以BC、PC的长为半径作圆弧,两弧交于点C′.
③连接BC′、DC′,得四边形ABC′D.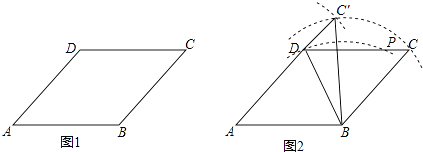
依据上述作图过程,解决以下问题:
(1)求证:∠A=∠C′;AD=BC′.
(2)根据作图过程和(1)中的结论,说明命题“有三条边相等且有一组对顶角相等的四边形是菱形”是命题.(填写“真”或“假”)
【答案】
(1)证明:连接BP,如图所示:
∵四边形ABCD是菱形,
∴AD=BC,∠A=∠BCD,
根据题意得:BC=B′C,BD=BP,DC′=PC,
∴AD=BC′,
在△BPC和△BDC′中,
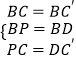 ,
,
∴△BPC≌△BDC′(SSS),
∴∠BCD=∠C′,
∴∠A=∠C′
(2)假
【解析】证明:(2)由(1)可知四边形ABC′D中,AB=AD=BC′,∠A=∠C,但四边形ABC′D不是菱形,
所以有三条边相等且有一组对顶角相等的四边形是菱形”是假命题,
所以答案是:假.
【考点精析】掌握菱形的判定方法和命题与定理是解答本题的根本,需要知道任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;我们把题设、结论正好相反的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题;经过证明被确认正确的命题叫做定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目