ЬтФПФкШн
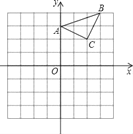
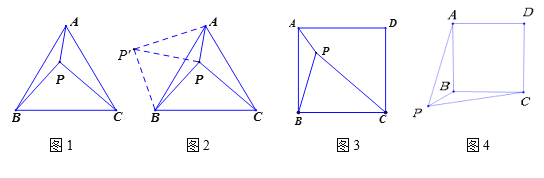
ЁОЬтФПЁПЃЈЮЪЬтЬсГіЃЉдкЪ§бЇЁАЙВЩњПЮЬУЁБЩЯЃЌФГКЯзїаЁзщЬсГіСЫетбљвЛИіЮЪЬтЃКШчЭМ1ЃЌдкЕШБпШ§НЧаЮABCФкгавЛЕуPЃЌЧвPAЃН1ЃЌPBЃН2ЃЌPCЃН![]() ЃЎФуФмЧѓГіЁЯAPBЕФЖШЪ§Т№ЃП
ЃЎФуФмЧѓГіЁЯAPBЕФЖШЪ§Т№ЃП
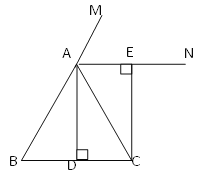
ЃЈЮЪЬтНтОіЃЉЃЈ1ЃЉРюЧхЭЌбЇЗжЮіЬтФПКѓЃЌЗЂЯжвдPAЁЂPBЁЂPCЕФГЄЮЊБпЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЃЌЫћевЕНСЫе§ШЗЕФЫМТЗЃКШчЭМ2ЃЌНЋЁїBPCШЦЕуBФцЪБеыа§зЊ60ЁуЃЌЕУЕНЁїBPЁфAЃЎСЌНгPPЁфЃЌвзЕУЁїPЁфPBЪЧЕШБпШ§НЧаЮЃЌЁїPЁфPAЪЧжБНЧШ§НЧаЮЃЌдђЕУЁЯBPPЁфЃН_________ЃЌЁЯAPBЃН_________ЃЎ
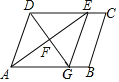
ЃЈЮЪЬтРрБШЃЉЃЈ2ЃЉЭЌзщЕФЦюЯьЭЌбЇЭЛШЛЯыЦ№дјОНтОіЙ§ЕФвЛИіЮЪЬтЃКШчЭМ3ЃЌЕуPЪЧе§ЗНаЮABCDФквЛЕуЃЌPA=1ЃЌPB=2ЃЌPC=3ЃЎЧѓЁЯAPBЕФЖШЪ§ЃЎЧыФуаДГіНтД№Й§ГЬЃЎ
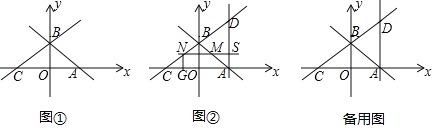
ЃЈЮЪЬтбгЩьЃЉЃЈ3ЃЉЯФРЯЪІСєСЫвЛИіЫМПМЬтЃКШчЭМ4ЃЌШєЕуPЪЧе§ЗНаЮABCDЭтвЛЕуЃЌPA=![]() ЃЌPB=1ЃЌPC=
ЃЌPB=1ЃЌPC=![]() ЃЎдђЁЯAPBЕФЖШЪ§ЃЎЧыФуаДГіНтД№Й§ГЬЃЎ
ЃЎдђЁЯAPBЕФЖШЪ§ЃЎЧыФуаДГіНтД№Й§ГЬЃЎ
ЁОД№АИЁПЃЈ1ЃЉ60ЁуЃЌ150ЁуЃЛЃЈ2ЃЉЁЯAPBЃН135ЁуЃЌМћНтЮіЃЛЃЈ3ЃЉЁЯAPBЃН45ЁуЃЌМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉНЋЁїBPCШЦЕуBФцЪБеыа§зЊ60ЁуЃЌЕУЕНЁїBPЁфAЃЌСЌНгPPЁфЃЌдђга![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЪЧЕШБпШ§НЧаЮЃЌдђга
ЪЧЕШБпШ§НЧаЮЃЌдђга![]() ЃЌ
ЃЌ![]() ЃЌПЩжЄ
ЃЌПЩжЄ![]() ЪЧжБНЧШ§НЧаЮЃЌРћгУ
ЪЧжБНЧШ§НЧаЮЃЌРћгУ![]() ПЩЕУД№АИЃЎ
ПЩЕУД№АИЃЎ
ЃЈ2ЃЉНЋ![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЃЌЕУЕНЁї
ЃЌЕУЕНЁї![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌИљОнЙДЙЩЖЈРэЕУЃЌ
ЃЌИљОнЙДЙЩЖЈРэЕУЃЌ![]() ЃЌПЩвджЄЕУ
ЃЌПЩвджЄЕУ![]() ЃЌМД
ЃЌМД![]() ЪЧжБНЧШ§НЧаЮЃЌЧв
ЪЧжБНЧШ§НЧаЮЃЌЧв![]() ЃЌ
ЃЌ
РћгУ![]() ПЩЕУД№АИЃЎ
ПЩЕУД№АИЃЎ
ЃЈ3ЃЉНЋ![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЃЌЕУЕНЁї
ЃЌЕУЕНЁї![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌИљОнЙДЙЩЖЈРэЕУЃЌ
ЃЌИљОнЙДЙЩЖЈРэЕУЃЌ![]() ЃЌПЩжЄЕУ
ЃЌПЩжЄЕУ![]() ЃЌМД
ЃЌМД![]() ЪЧжБНЧШ§НЧаЮЃЌЧв
ЪЧжБНЧШ§НЧаЮЃЌЧв![]() ЃЌ
ЃЌ
РћгУ![]() ПЩЕУД№АИЃЎ
ПЩЕУД№АИЃЎ
НтЃКЃЈ1ЃЉНЋЁїBPCШЦЕуBФцЪБеыа§зЊ60ЁуЃЌЕУЕНЁїBPЁфAЃЌСЌНгPPЁфЃЌ
дђга![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЪЧЕШБпШ§НЧаЮЃЌ
ЪЧЕШБпШ§НЧаЮЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]()
Ёр![]() ЪЧжБНЧШ§НЧаЮЃЌ
ЪЧжБНЧШ§НЧаЮЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМЪОЃЌНЋ![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЃЌЕУЕНЁї
ЃЌЕУЕНЁї![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ
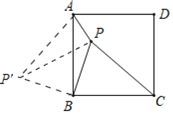
дђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
![]() ЃЌ
ЃЌ
ИљОнЙДЙЩЖЈРэЕУЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
гж![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЪЧжБНЧШ§НЧаЮЃЌЧв
ЪЧжБНЧШ§НЧаЮЃЌЧв![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
ЃЈ3ЃЉШчЭМЪОЃЌНЋ![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЃЌЕУЕНЁї
ЃЌЕУЕНЁї![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎ
ЃЎ
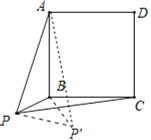
дђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
![]() ЃЌ
ЃЌ
ИљОнЙДЙЩЖЈРэЕУЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
гж![]()
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЪЧжБНЧШ§НЧаЮЃЌЧв
ЪЧжБНЧШ§НЧаЮЃЌЧв![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ