题目内容
【题目】四边形具有不稳定性，如图，在平面直角坐标系
中，矩形
的边
在
轴上，且点
，边
长为
．现固定边，向右推动矩形使点
落在
轴上(落点记为
)，点
的对应点记为
，已知矩形与推动后形成的平行四边形
的面积比为
，则点坐标为_______．
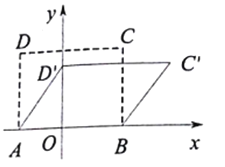
【答案】（7，4）
【解析】
根据面积比可求出OD′的长，利用勾股定理可求出OA的长，根据点B坐标可得OB的长，即可求出AB的长，根据平行四边形的性质可得C′D′=AB，即可得答案．
∵固定边
，向右推动矩形使点
落在
轴上，AD=5，
∴AD′=AD=5，
∵矩形
与推动后形成的平行四边形
的面积比为
，
∴
，
∴OD′=4，
∴OA=
=3，
∵点B坐标为（4，0），
∴OB=4，
∴AB=OB+OA=7，
∴C′D′=AB=7，
∴点C′的坐标为（7，4）
故答案为：（7，4）
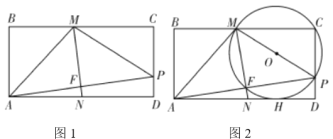
【题目】如图，在矩形
中，
是
延长线上的定点，
为
边上的一个动点，连接
，将射线绕点顺时针旋转
，交射线
于点
，连接
．
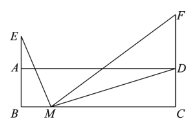
小东根据学习函数的经验，对线段
的长度之间的关系进行了探究．
下面是小东探究的过程，请补充完整：
（1）对于点在上的不同位置，画图、测量，得到了线段的长度的几组值，如下表：
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | |
| 0.00 | 0.53 | 1.00 | 1.69 | 2.17 | 2.96 | 3.46 | 3.79 | 4.00 |
| 0.00 | 1.00 | 1.74 | 2.49 | 2.69 | 2.21 | 1.14 | 0.00 | 1.00 |
| 4.12 | 3.61 | 3.16 | 2.52 | 2.09 | 1.44 | 1.14 | 1.02 | 1.00 |
在的长度这三个量中，确定_____的长度是自变量，_____的长度和_____的长度都是这个自变量的函数；
（2）在同一平面直角坐标系
中，画出（1）中所确定的两个函数的图象；
（3）结合画出的函数图象，解决问题：当
时，
的长度约为________
．
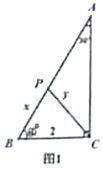
【题目】数学活动课上，小明同学根据学习函数的经验，对函数的图像、性质进行了探究，下面是小明同学探究过程，请补充完整：
如图1，已知在
，
，
，
，点
为
边上的一个动点，连接
．设
，
．
（初步感知）
（1）当
时，则①
________，②
________；
（深入思考）
（2）试求
与
之间的函数关系式并写出自变量的取值范围；
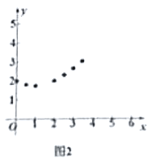
（3）通过取点测量，得到了与的几组值，如下表：
| 0 | 0.5 | 1 | 1.5 | 2. | 2.5 | 3 | 3.5 | 4 |
| 2 | 1.8 | 1.7 | _____ | 2 | 2.3 | 2.6 | 3.0 | _____ |
（说明：补全表格时相关数值保留一位小数）
1）建立平面直角坐标系，如图2，描出已补全后的表中各对应值为坐标的点，画出该函数的图象；
2）结合画出的函数图象，写出该函数的两条性质：
①________________________________；②________________________________．
