题目内容
【题目】小民对函数![]() 的图象和性质进行了探究.已知当自变量
的图象和性质进行了探究.已知当自变量![]() 的值为
的值为![]() 时,函数值为
时,函数值为![]() ;当自变量的值为
;当自变量的值为![]() 时,函数值为
时,函数值为![]() .探究过程如下,请补充完整,
.探究过程如下,请补充完整,
(1)求这个函数的表达式;
(2)在给出的平面直角坐标系中画出这个函数的图象并写出这个函数的一条性质:___________;
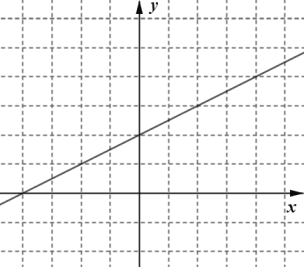
(3)进一步探究函数图象并解决问题:已知函数![]() 的图象如图所示,请结合你所画的函数图象,直接写出不等式
的图象如图所示,请结合你所画的函数图象,直接写出不等式![]() 的解集:___________.
的解集:___________.
【答案】(1)y1=|x-2|+![]() |x|;(2)当x=2时,此函数有最小值1;(3)x≥4或x≤0.
|x|;(2)当x=2时,此函数有最小值1;(3)x≥4或x≤0.
【解析】
(1)把(1,![]() ),(-1,
),(-1,![]() )代入
)代入![]() 可得关于a、b的二元一次方程组,解方程组求出a、b的值即可得答案;
可得关于a、b的二元一次方程组,解方程组求出a、b的值即可得答案;
(2)分x<0,0≤x<2,x≥2三种情况,分别利用描点法画出图象,根据图象写出相关性质即可;
(3)根据图象找出![]() 的图象在
的图象在![]() 图象上方的部分所对应的x的取值范围即可.
图象上方的部分所对应的x的取值范围即可.
(1)∵当自变量![]() 的值为
的值为![]() 时,函数值为
时,函数值为![]() ;当自变量的值为
;当自变量的值为![]() 时,函数值为
时,函数值为![]() ,
,
∴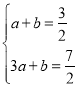 ,
,
解得:![]() ,
,
∴这个函数的表达式为y1=|x-2|+![]() |x|.
|x|.
(2)列表如下:
x | …… | -2 | -1 | 0 | 1 | 2 | 3 | 4 | …… |
y1 | …… | 5 |
| 2 |
| 1 |
| 4 | …… |
当x<0时,y1=![]() x+2,
x+2,
当0≤x<2时,y1=![]() x+2,
x+2,
当x≥2时,y1=![]() x-2,
x-2,
∴描点画图如下:
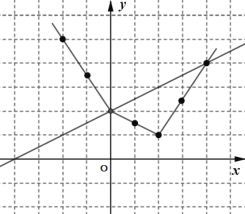
由图象可知:当x=2时,此函数有最小值1.
(3)由图象可知:x≥4或x≤0时,![]() 的图象在
的图象在![]() 图象上方,
图象上方,
∴不等式![]() 的解集为:x≥4或x≤0.
的解集为:x≥4或x≤0.
故答案为:x≥4或x≤0

【题目】十九大召开后,某社区开展了“市民对十九大的关注情况”调查,采用随机抽样的方法访问了部分年龄在18周岁以上的城乡居民.小聪根据调查数据绘制了如下不完整的频数分布置表和扇形统计图.请根据图表解答下列问题.
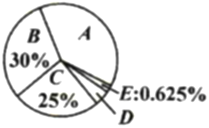
关注情况 | 频数 |
非常关注( | 128 |
比较关注( | |
一般关注( | 80 |
不太关注( | |
不关注( | 2 |
(1)请完成频数分布表空格数据填写;
(2)求“非常关注”部分扇形圆心角的度数;
(3)若该社区18周岁以上居民共有20000人,请估计“比较关注”和“非常关注”的居民共有多少人?