题目内容
 已知:如图,一次函数y=
已知:如图,一次函数y=| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(1)求二次函数的解析式;
(2)求四边形BDEC的面积S;
(3)在x轴上有一动点P,从O点出发以每秒1个单位的速度沿x轴向右运动,是否存在点P使得△PBC是以P为直角顶点的直角三角形?若存在,求出点P运动的时间t的值,若不存在,请说明理由.
(4)若动点P在x轴上,动点Q在射线AC上,同时从A点出发,点P沿x轴正方向以每秒2个单位的速度运动,点Q以每秒a个单位的速度沿射线AC运动,是否存在以A、P、Q为顶点的三角形与△ABD相似,若存在,求a的值,若不存在,说明理由.
分析:(1)根据直线BC的解析式,可求得点B的坐标,由于B、D都在抛物线的图象上,那么它们都满足该抛物线的解析式,通过联立方程组即可求得待定系数的值;
(2)根据抛物线的解析式,可求得E点的坐标,联立直线BC的解析式,可求得C点坐标;那么四边形BDEC的面积即可由△AEC、△ABD的面积差求得;
(3)假设存在符合条件的P点,连接BP、CP,过C作CF⊥x轴于F,若∠BPC=90°,则△BPO∽△CPF,可设出点P的坐标,分别表示出OP、PF的长,根据相似三角形所得比例线段即可求得点P的坐标,继而得出t的值.
(4)假设成立有△ABD∽△APQ或△ABD∽△AQP,则有∠ABD=∠APQ,或∠ABD=∠AQP,判断是否满足即可.
(2)根据抛物线的解析式,可求得E点的坐标,联立直线BC的解析式,可求得C点坐标;那么四边形BDEC的面积即可由△AEC、△ABD的面积差求得;
(3)假设存在符合条件的P点,连接BP、CP,过C作CF⊥x轴于F,若∠BPC=90°,则△BPO∽△CPF,可设出点P的坐标,分别表示出OP、PF的长,根据相似三角形所得比例线段即可求得点P的坐标,继而得出t的值.
(4)假设成立有△ABD∽△APQ或△ABD∽△AQP,则有∠ABD=∠APQ,或∠ABD=∠AQP,判断是否满足即可.
解答: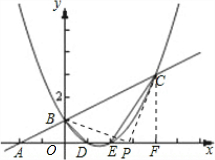 解:(1)将B(0,1),D(1,0)的坐标代入y=
解:(1)将B(0,1),D(1,0)的坐标代入y=
x2+bx+c,
得:
,
解得:
故解析式y=
x2-
x+1;
(2)设C(x0,y0),
则有
,
解得
,
∴C(4,3),
由图可知:S=S△ACE-S△ABD,又由对称轴为x=
可知E(2,0),
∴S=
AE•y0-
AD×OB=
×4×3-
×3×1=
;
(3)设符合条件的点P存在,令P(a,0):
当P为直角顶点时,如图:过C作CF⊥x轴于F;
∵Rt△BOP∽Rt△PFC,
∴
=
,
即
=
,
整理得a2-4a+3=0,
解得a=1或a=3;
故可得t=1或3.
(4)存在符合条件的t值,使△APQ与△ABD相似,
①当△APQ∽△ABD时,
=
,
解得:a=
;
②当
=
解得:a=
,
∴存在符合条件的a值,使△APQ与△ABD相似,a=
或
.
 解:(1)将B(0,1),D(1,0)的坐标代入y=
解:(1)将B(0,1),D(1,0)的坐标代入y=| 1 |
| 2 |
得:
|
解得:
|
故解析式y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)设C(x0,y0),
则有
|
解得
|
∴C(4,3),
由图可知:S=S△ACE-S△ABD,又由对称轴为x=
| 3 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
(3)设符合条件的点P存在,令P(a,0):
当P为直角顶点时,如图:过C作CF⊥x轴于F;
∵Rt△BOP∽Rt△PFC,
∴
| BO |
| PF |
| OP |
| CF |
即
| 1 |
| 4-a |
| a |
| 3 |
整理得a2-4a+3=0,
解得a=1或a=3;
故可得t=1或3.
(4)存在符合条件的t值,使△APQ与△ABD相似,
①当△APQ∽△ABD时,
| AP |
| AB |
| AQ |
| AD |
解得:a=
| 4 |
| 3 |
②当
| AP |
| BD |
| PQ |
| AB |
解得:a=
| 20 |
| 7 |
∴存在符合条件的a值,使△APQ与△ABD相似,a=
| 4 |
| 3 |
| 20 |
| 7 |
点评:此题考查了二次函数解析式的确定、函数图象交点坐标及图形面积的求法、直角三角形的判定以及相似三角形的性质等,难度适中.

练习册系列答案
相关题目
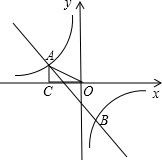 知
知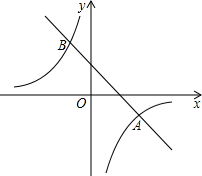 (2013•白云区一模)已知,如图,一次函数y=kx+b的图象与反比例函数y=
(2013•白云区一模)已知,如图,一次函数y=kx+b的图象与反比例函数y= 已知:如图,一次函数y=kx+b的图象与反比例函数
已知:如图,一次函数y=kx+b的图象与反比例函数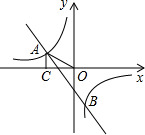 OA=
OA=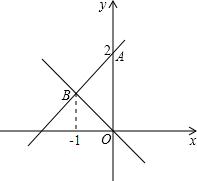 已知:如图,一次函数y=kx+b的图象与y轴交于点A,且与正比例函数y=-x的图象交于点B,则该一次函数的解析式为
已知:如图,一次函数y=kx+b的图象与y轴交于点A,且与正比例函数y=-x的图象交于点B,则该一次函数的解析式为