Question

【题目】如图，已知：AB为⊙O直径，PQ与⊙O交于点C，AD⊥PQ于点D，且AC为∠DAB的平分线，BE⊥PQ于点E．

（1）求证：PQ与⊙O相切；

（2）求证：点C是DE的中点．

Answer 1

【答案】（1）见解析；（2）见解析．

【解析】

（1）连接OC，由角平分线的性质和等腰三角形的性质可得∠DAC＝∠ACO，可得AD∥OC，由平行线的性质可得OC⊥PQ，可得结论；

（2）由平行线分线段成比例可得DC＝CE，即点C是DE的中点．

证明：（1）连接OC，

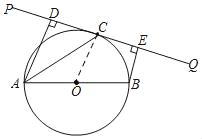
∵AC平分∠DAB

∴∠DAC＝∠CAO，

∵OA＝OC，

∴∠OAC＝∠OCA

∴∠DAC＝∠ACO

∴AD∥OC，且AD⊥PQ

∴OC⊥PQ，且OC为半径

∴PQ与⊙O相切

（2）∵OC⊥PQ，AD⊥PQ，BE⊥PQ

∴OC∥AD∥BE

∴

∴DC＝CE

∴点C是DE的中点．