Question

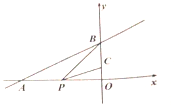
【题目】如图，在平面直角坐标系中，直线不经过第四象限，且与轴，轴分别交于两点，点为的中点，点在线段上，其坐标为，连结，，若，那么的值为（ ）

A. B. 4C. 5D. 6

Answer 1

【答案】D

【解析】

典型的“一线三等角”，构造相似三角形△AOB∽△DPC,即可证明△PCD∽△BPA，由相似比求得边的相应关系，从而求解．

解：在x轴上找点D（4,0），连接CD.

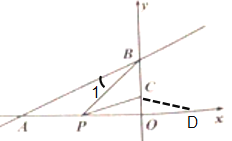
由可得A(-2m，0 )，B(0，m )，直线不经过第四象限，所以m>0,

所以OA=2m，OB=m；因为坐标为，点D（4,0）所以OC=2，OD=4,

因为,∠AOB=∠DOC=90° ,所以△AOB∽△DPC,所以∠CDO=∠BAO.

又因为，所以根据三角形内角和和平角定义可得：∠APB+∠1=∠APB+∠CPD

所以∠1=∠CPD，又因为∠CDO=∠BAO，所以△PCD∽△BPA，所以 ,

因为点为的中点，所以AP=OP=m，PD=m+4，Rt△AOB中，由勾股定理得AB= m，同理得CD=2，因为，所以，解得m=6.

故选：D.