题目内容
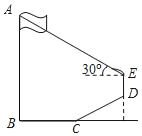
【题目】如图，为测量学校旗杆AB的高度，小明从旗杆正前方6米处的点C出发，沿坡度为i＝1：
的斜坡CD前进2米到达点D，在点D处放置测角仪DE，测得旗杆顶部A的仰角为30°，量得测角仪DE的高为1.5米．A、B、C、D、E在同一平面内，且旗杆和测角仪都与地面垂直．
(1)求点D的铅垂高度(结果保留根号)；
(2)求旗杆AB的高度(结果保留根号)．
【答案】（1）
米（2）（4+1.5）米
【解析】
（1）延长ED交射线BC于点H．由题意得DH⊥BC．解直角三角形即可得到结论；
（2）过点E作EF⊥AB于F．得到∠AEF=30°．推出四边形FBHE为矩形．根据矩形的性质得到EF=BH=BC+CH=9．解直角三角形即可得到结论．
（1）延长ED交射线BC于点H．
由题意得：DH⊥BC．
在Rt△CDH中，∠DHC=90°，tan∠DCH=i=1：
，∴∠DCH=30°，∴CD=2DH．
∵CD=2，∴DH
，CH=3．
答：点D的铅垂高度是米．
（2）过点E作EF⊥AB于F．
由题意得：∠AEF即为点E观察点A时的仰角，∴∠AEF=30°．
∵EF⊥AB，AB⊥BC，ED⊥BC，∴∠BFE=∠B=∠BHE=90°，∴四边形FBHE为矩形，∴EF=BH=BC+CH=9，FB=EH=ED+DH=1.5
．
在Rt△AEF中，∠AFE=90°，AF=EFtan∠AEF=9
，∴AB=AF+FB=3
1.5．
答：旗杆AB的高度约为（4
1.5）米．
练习册系列答案
相关题目
