Question

【题目】如图，已知△ABC中，AB＝AC，把△ABC绕A点沿顺时针方向旋转得到△ADE，连接BD，CE交于点F.

(1)求证：△AEC≌△ADB；

(2)若AB＝2，∠BAC＝45°，当四边形ADFC是菱形时，求BF的长．

Answer 1

【答案】（1）证明见解析（2）2-2

【解析】试题分析：

（1）由旋转的性质易得：AD=AB，AE=AC，∠DAE=∠BAC，结合已知和图形可得AD=AC=AB=AE，∠EAC=∠DAB，再由“SAS”可证△AEC≌△ADB；

（2）由四边形ADFC是菱形可得DF=AC=AB=2，AC∥DF，从而可得∠DBA=∠BAC=45°，再由AD=AB可得∠BDA=∠DBA=45°，就能证明△ADB是等腰直角三角形，由勾股定理可得BD的长，最后由BD-DF可得BF的长.

试题解析：

(1)由旋转的性质得△ABC≌△ADE，且AB＝AC，

∴AE＝AD＝AC＝AB，∠BAC＝∠DAE，

∴∠BAC＋∠BAE＝∠DAE＋∠BAE，即∠CAE＝∠BAD.

∵在△AEC和△ADB中， ，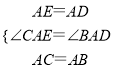

∴△AEC≌△ADB(SAS)；

(2)∵四边形ADFC是菱形，

∴DF＝AC＝AB＝2，AC∥DF.

∴∠DBA＝∠BAC＝45°.

由(1)可知AB＝AD，

∴∠DBA＝∠BDA＝45°，

∴△ABD为直角边长为2的等腰直角三角形，

∴BD2＝AB2+AD2，即BD2＝8，解得BD=，

∴BF＝BD－DF＝－2.