题目内容
【题目】如图1,在矩形ABCD中,点A(1,1),B(3,1),C(3,2),反比例函数y=![]() (x>0)的图象经过点D,且与AB相交于点E,
(x>0)的图象经过点D,且与AB相交于点E,
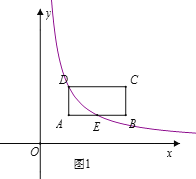
(1)求反比例函数的解析式;
(2)过点C、E作直线,求直线CE的解析式;
(3)如图2,将矩形ABCD沿直线CE平移,使得点C与点E重合,求线段BD扫过的面积.

【答案】(1)反比例函数的解析式为y=![]() ; (2)直线CE的解析式为y=x-1;(3) 3.
; (2)直线CE的解析式为y=x-1;(3) 3.
【解析】分析:(1)由矩形的性质求得点D的坐标,即可求得k;(2)根据反比例函数的解析式求点E的坐标,用待定系数法求直线CE的解析式;(3)BD扫过的面积是一个平行四边形,它的面积=2S△BB′D′.
详解:(1)由题意得AD=CB=1,故点D的坐标为(1,2),
∵函数y=![]() 的图象经过点D(1,2),
的图象经过点D(1,2),
∴2=![]() .∴m=2,
.∴m=2,
∴反比例函数的解析式为y=![]() ;
;
(2)当y=1时,1=![]() .∴x=2,∴E(2,1),
.∴x=2,∴E(2,1),
设直线CE的解析式为y=kx+b,根据题意得![]()
解得![]()
∴直线CE的解析式为y=x-1;
(3)∵矩形ABCD沿直线CE平移,使得点C与点E重合,点D(0,1),B'(2,0),
S四边形BDD′B′=2S△BB′D′=2×![]() ×3×1=3.
×3×1=3.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目