题目内容
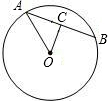
如图，AB，AC分别是⊙O的直径和弦，OD⊥AC于点D，连接BD、BC，AB=5，AC=4，
求：BD的长．
求：BD的长．
∵OD过圆心O，OD⊥AC，AC=4，
∴CD=
AC=2，
∵AB是⊙O的直径，
∴∠C=90°，
∴BC=
=
=3，
在Rt△BCD中，
DB=
=
=
．
故答案为：
．
∴CD=
| 1 |
| 2 |
∵AB是⊙O的直径，
∴∠C=90°，
∴BC=
| AB2-AC2 |
| 52-42 |
在Rt△BCD中，
DB=
| BC2+CD2 |
| 32+22 |
| 13 |
故答案为：
| 13 |
练习册系列答案
名校课堂系列答案
相关题目
