题目内容
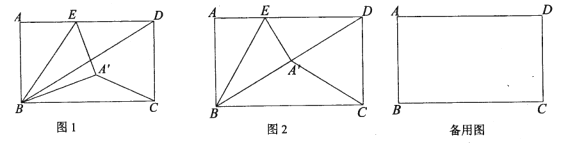
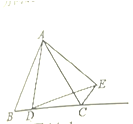
【题目】在平面直角坐标系
中（如图），已知抛物线
经过原点，与
轴的另一个交点为
，顶点为
.
（1）求这条抛物线表达式；
（2）将该抛物线向右平移，平移后的新抛物线顶点为
，它与
轴交点为
，联结
、
，设点
的纵坐标为
，用含的代数式表示
的正切值；
（3）联结
，在（2）的条件下，射线
平分
，求点到直线的距离.
【答案】（1）
；（2）
；（3）6
【解析】
可设顶点式解析式，把点
代入，求得a，从而得抛物线的解析式；
画图，把
放到直角三角形中来考虑，分别用点P、点H、点B的相关坐标来表示这个直角三角形中的直角边长即可求解；
设PB与x轴交于点M，求出点A坐标，利用点P坐标，得出AP长度，利用角平分线即
轴，推得
，从而得出AP和AM的长度；
求出直线PB得解析式，从而求得点B的坐标，进而求出BH的长度，再利用角平分线的性质定理即可得点B到直线AP的距离就等于BH的长度．
解：设抛物线表达式为：
把代入得
，
抛物线的表达式：
．
设PQ与y轴交点为H．
，
，
，
，
在
中，
．
故的正切值为：
．
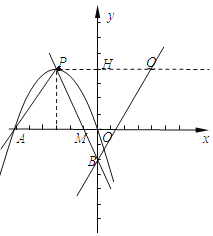
设PB与x轴交于点M．
由得点A坐标为
．
又
，
．
射线PB平分
，
．
轴，
，
，
，
．
设直线PB为
，把点，
代入，得：
，
点B为
．
．
射线PB平分，
，
点B到直线AP的距离为6．
练习册系列答案
相关题目
