题目内容
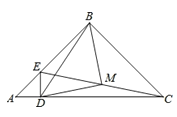
【题目】已知在△ABC中,AB=BC=8cm,∠ABC=90°,点E以每秒1cm/s的速度由A向点B运动,ED⊥AC于点D,点M为EC的中点.
(1)求证:△BMD为等腰直角三角形;
(2)当点E运动多少秒时,△BMD的面积为12.5cm2?
【答案】(1)证明见解析;(2)2.
【解析】试题分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得BM=![]() CE,DM=
CE,DM=![]()
CE,得出BM=DM,再由等腰三角形的性质和三角形的外角性质证出∠BMD=90°即可;
(2)由等腰直角三角形的面积求出BM,得出CE,由勾股定理求出BE,得出AE,即可得出结果.
试题解析:(1)∵∠ABC=90°,DE⊥AC,点M为EC的中点,AB=BC,
∴BM=![]() CE=CM,DM=
CE=CM,DM=![]() CE=CM,∠BAC=∠ACB=45°,
CE=CM,∠BAC=∠ACB=45°,
∴BM=DM,∠MBC=∠MCB,∠MDC=∠MCD,
∵∠BME=∠MBC+∠MCB,∠DME=∠MDC+∠MCD,∠MCB+∠MCD=∠ACB=45°,
∴∠BMD=∠BME+∠DME=45°+45°=90°,
∴△BMD为等腰直角三角形;
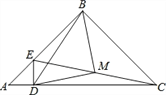
(2)由(1)得:△BMD为等腰直角三角形,
∴△BMD的面积=![]() BMDM=
BMDM= ![]() BM2=12.5,解得:BM=5,
BM2=12.5,解得:BM=5,
∴CE=2BM=10cm,由勾股定理得:BE= ![]() =6(cm),
=6(cm),
∴AE=AB﹣BE=2cm,∴2÷1=2(s),
即当点E运动2秒时,△BMD的面积为12.5cm2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目