ЬтФПФкШн
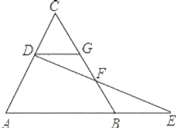
ЁОЬтФПЁПдкОиаЮABCDжаЃЌAB=4cmЃЌBC=8cm,ЖЏЕуPДгЕуAГіЗЂЃЌвд1cm/sЕФЫйЖШбиABЯђЕуBдЫЖЏЃЌЖЏЕуQДгЕуBГіЗЂЃЌвд2cm/sУыЕФЫйЖШбиBCЯђЕуCдЫЖЏ.PЁЂQЗжБ№ДгAЁЂBЭЌЪБГіЗЂЃЌЩшдЫЖЏЪБМфЮЊtУы.(ШчЭМ1)

ЃЈЃБЃЉгУКЌtЕФДњЪ§ЪНБэЪОЯТСаЯпЖЮГЄЖШЃК
ЂйPB=__________cm,ЂкQB=_____cm,ЂлCQ=_________cm.
(2)ЕБЁїPBQЕФУцЛ§ЕШгк3![]() ЪБЃЌЧѓtЕФжЕ.
ЪБЃЌЧѓtЕФжЕ.
(3) (ШчЭМ2)ЃЌШєEЮЊБпCDжаЕуЃЌСЌНсEQЁЂAQ.ЕБвдAЁЂBЁЂQЮЊЖЅЕуЕФШ§НЧаЮгыЁїEQCЯрЫЦЪБЃЌжБНгаДГіТњзуЬѕМўЕФtЕФЫљгажЕ.
ЁОД№АИЁПЃЈ1ЃЉPB=4-tЃЛQB=2tЃЛCQ=8-2tЃЛЃЈ2ЃЉ1Лђ3ЃЛЃЈ3ЃЉ![]() Лђ
Лђ![]() Лђ
Лђ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтаДГіНсЙћМДПЩЃЛ
ЃЈ2ЃЉРћгУШ§НЧаЮЕФУцЛ§ЙЋЪНСаЗНГЬЧѓНтМДПЩЃЛ
ЃЈ3ЃЉИљОнЯрЫЦШ§НЧаЮЕФаджЪЃЌЗжСНжжЧщПіСаЪНЧѓНтМДПЩ.
ЃЈ1ЃЉгЩЬтвтЕУЃЌ
ЂйPB=4-tЃЛЂкQB=2tЃЛЂлCQ=8-2tЃЛ
ЃЈ2ЃЉЁпЁїPBQЕФУцЛ§ЕШгк3![]() ЃЌ
ЃЌ
Ёр2t(4-t)=3ЁС2,
НтжЎЕУЃЌ
t=1Лђ3ЃЛ
ЃЈ3ЃЉЕБЁїABQЁЋЁїQCEЪБЃЌ
![]() ,
,
Ёр![]() ,
,
НтжЎЕУЃЌ
x1=![]() ЃЌx2=
ЃЌx2=![]() ;
;
ЕБЁїABQЁЋЁїECQEЪБЃЌ
![]() ,
,
Ёр![]() ,
,
НтжЎЕУЃЌ
t=![]() .
.
ЁрТњзуЬѕМўЕФtЕФЫљгажЕЮЊ![]() Лђ
Лђ![]() Лђ
Лђ![]() .
.

 ПьРжЪюМйЪюМйФмСІздВтжаЮїЪщОжЯЕСаД№АИ
ПьРжЪюМйЪюМйФмСІздВтжаЮїЪщОжЯЕСаД№АИ