Question

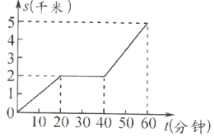
【题目】甲、乙两人同时从A地前往相距5千米的B地.甲骑自行车，途中修车耽误了20分钟，甲行驶的路程（千米）关于时间（分钟）的函数图像如图所示；乙慢跑所行的路程（千米）关于时间（分钟）的函数解析式为.

（1）在图中画出乙慢跑所行的路程关于时间的函数图像；

（2）乙慢跑的速度是每分钟________千米；

（3）甲修车后行驶的速度是每分钟________千米；

（4）甲、乙两人在出发后，中途________分钟时相遇.

Answer 1

【答案】（1）图像见解析；（2）；（3）；（4）24.

【解析】

（1）根据所给解析式可知函数过原点，并过点（60，5），由这两点即可得出答案．

（2）乙慢跑的速度即是乙慢跑所行的路程s（千米）关于时间t（分钟）的函数解析式的斜率；

（3）甲修车后行驶路程是3km，所用时间是20min，即可求出速度；

（4）甲乙相遇，体现在（1）中的图形即是它们的交点，即求出交点得出答案．

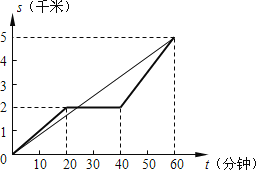
（1）所画图形如下所示：

（2）乙慢跑的速度为:千米/分钟；

（3）甲修车后行驶20min，所形路程为3km，

故甲修车后行驶的速度为：3÷20=km/min；

（4）由甲行驶的路程s（千米）关于时间t（分钟）的函数图象与乙慢跑所行的路程s（千米）关于时间t（分钟）的函数图象可知：

在距离A地2km处甲乙相遇，此时乙行驶了2×12=24分钟，

即甲、乙两人在出发后，中途24分钟时相遇．