题目内容
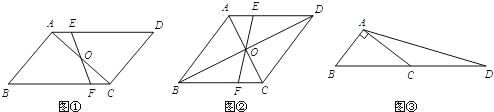
【题目】猜想:如图①,在ABCD中,点O是对角线AC的中点,过点O的直线分别交AD、BC于点E、F.若ABCD的面积是10,则四边形CDEF的面积是 .
探究:如图②,在菱形ABCD中,对角线AC、BD相交于点O,过点O的直线分别交AD、BC于点E、F.若AC=4,BD=8,求四边形ABFE的面积.
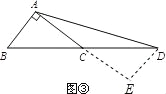
应用:如图③,在Rt△ABC中,∠BAC=90°,延长BC到点D,使DC=BC,连结AD.若AC=4,![]() ,则△ABD的面积是 .
,则△ABD的面积是 .
【答案】5;8;12
【解析】
试题分析:猜想:首先根据平行四边形的性质可得AD∥BC,OA=OC.根据平行线的性质可得∠EAO=∠FCO,∠AEO=∠CFO,进而可根据AAS定理证明△AEO≌△CFO,再根据全等三角形的性质可得结论;
探究:根据菱形的性质得到AD∥BC,AO=CO,BO=![]() BD=4,根据全等三角形的判定定理得到△AOE≌△COF,由于AC⊥BD,于是得到结果;
BD=4,根据全等三角形的判定定理得到△AOE≌△COF,由于AC⊥BD,于是得到结果;
应用:延长AC到E使CE=AC=4,根据全等三角形的判定定理得到△ABC≌△CDE,由全等三角形的性质得到∠E=∠BAC=90°,根据勾股定理得到DE=![]() =3,即可得到结论.
=3,即可得到结论.
试题解析:猜想:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC.
∴∠EAO=∠FCO,∠AEO=∠CFO,
在△AOE和△COF中,
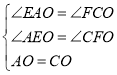 ,
,
∴△AEO≌△CFO,
∴四边形CDEF的面积=S△ACD=![]() ABCD的面积=5;
ABCD的面积=5;
探究:∵四边形ABCD是菱形,
∴AD∥BC,AO=CO,BO=![]() BD=4,
BD=4,
∴∠OAE=∠OCF,∠OEA=∠OFC,
在△AOE于△COF中,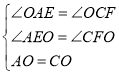 ,
,
∴△AOE≌△COF,
∵AC⊥BD,
∴![]() .
.
应用:延长AC到E使CE=AC=4,
在△ABC与△CDE中,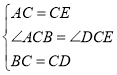 ,
,
∴△ABC≌△CDE,
∴∠E=∠BAC=90°,
∴DE=![]() =3,
=3,
∴S△ABD=S△ADE=![]() AEDE=
AEDE=![]() ×8×3=12.
×8×3=12.