��Ŀ����
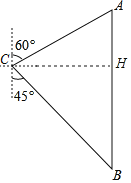
����Ŀ��һ�οͲ��дӱ���C�������ر�ƫ��60��ķ������ߵ�1000������A�����ιۺ��ִ�A�������Ϸ�������һ�ξ��뵽��λ�ڱ�����ƫ��45�㷽��ľ�ҵ��B������ͼ��ʾ��
��1���������οʹ���������ҵ�µ�;�е����ݵ���̾��룻
��2���������ο���80��/�ֵ��ٶȴӾ�ҵ�·��ر��ݣ���ô������10�����ڵ����������ͨ������˵�����ɣ��������ο����ߵ�·�߾�����ֱ�����ߵģ�

���𰸡���1�������ݵ���̾���Ϊ500![]() �ף���2�����ܵ�����ݣ�
�ף���2�����ܵ�����ݣ�
��������
��1������C��CH��AB��AB�ڵ�H���������Ǻ����Ķ��弴�ɵõ����ۣ�
��2���������Ǻ����Ķ���õ�![]() �����
�����![]() �����ǵõ����ۣ�
�����ǵõ����ۣ�
��1������C��CH��AB��AB�ڵ�H��
��Rt��ACH��
�ߡ�ACH��30����
��CH��1000cos30����1000��![]() ��
��
�𣺵����ݵ���̾���Ϊ500![]() �ף�
�ף�
��2����Rt��CHB����BCH��45����CH��500![]() ��
��
��BC��CH��cos45����500��![]() ��
��
��t��![]() ��
��
��ܵ�����ݣ�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ