题目内容
【题目】如图，在Rt△ABC中，∠ABC=90°，点D是AC的中点，作∠ADB的角平分线DE交AB于点E，AE=6，DE=10，点P在边BC上，且△DEP为等腰三角形，则BP的长为_____________
【答案】2或5或8或18
【解析】
根据直角三角形斜边上的中线等于斜边的一半可得BD=AD=
AC，再根据等腰三角形三线合一的性质可得DE⊥AB，AE=BE，然后分四种情况讨论求解.
如图，
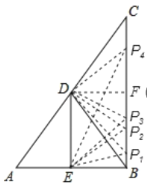
∵∠ABC=90°，点D是AC的中点
∴BD=AD=AC
∵DE是∠ADB的角平分线
∴DE⊥AB，AE=BE=6
①DE=DP1时，过点D作DF⊥BC于点F，
则DF=BE=6
由勾股定理得：
∴
②DP2=P2E时，
③DE=EP3时，
④DE=DP4时，
综上所述，BP的长为2、5、8、18
故答案为：2、5、8、18
练习册系列答案
导学与测试系列答案
新非凡教辅冲刺100分系列答案
相关题目
【题目】某校有2000名学生，为了解全校学生的上学方式，该校数学兴趣小组在全校随机抽取了150名学生进行抽样调查．整理样本数据，得到下列图表：
某校150名学生上学方式的分布表
方式 | 划记 | 人数 |
步行 | 正正正 | 15 |
骑车 | 正正正正正正 正正正正 | 51 |
乘公共交 通工具 | 正正正正正 正正正正 | 45 |
乘私家车 | 正正正正正正 | 30 |
其他 | 正 | 9 |
合计 | 150 |
(1)理解画线语句的含义，回答问题：如果150名学生全部在同一个年级抽取，那么这样的抽取是否合理？请说明理由．答：__________________________________.
(2)该校数学兴趣小组结合调查获取的信息，向学校提出了一些建议．如：骑车上学的学生数约占全校的34%，建议学校合理安排自行车停车场地．请你结合上述统计的全过程，再提出一条合理化建议：________________________.
