题目内容
(1)如图所示,已知△ABC中,∠ABC、∠ACB的平分线相交于点O.试说明∠BOC=90°+ ∠A;
∠A;
(2)如图所示,在△ABC中,BD、CD分别是∠ABC、∠ACB的外角平分线.试说明∠D=90°- ∠A;
∠A;
(3)如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,且与BD交于点D,试说明∠A=2∠D.
证明:(1)∵在△ABC中,OB、OC分别是∠ABC、∠ACB的平分线,∠A为x°
∴∠OBC+∠OCB= (180°-∠A)=
(180°-∠A)= ×(180°-x°)=90°-
×(180°-x°)=90°- ∠A
∠A
故∠BOC=180°-(∠OBC+∠OCB)=180°-(90°- ∠A)=90°+
∠A)=90°+ ∠A;
∠A;
(2)∵BD、CD为△ABC两外角∠ABC、∠ACB的平分线,∠A为x°
∴∠BCD= (∠A+∠ABC)、∠DBC=
(∠A+∠ABC)、∠DBC= (∠A+∠ACB),
(∠A+∠ACB),
由三角形内角和定理得,∠BDC=180°-∠BCD-∠DBC,
=180°- [∠A+(∠A+∠ABC+∠ACB)],
[∠A+(∠A+∠ABC+∠ACB)],
=180°- (∠A+180°),
(∠A+180°),
=90°- ∠A;
∠A;
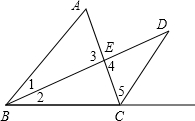
(3)如图:∵BD为△ABC的角平分线,交AC与点E,CD为△ABC外角∠ACE的平分线,两角平分线交于点D
∴∠1=∠2,∠5= (∠A+2∠1),∠3=∠4,
(∠A+2∠1),∠3=∠4,
在△ABE中,∠A=180°-∠1-∠3
∴∠1+∠3=180°-∠A----①
在△CDE中,∠D=180°-∠4-∠5=180°-∠3- (∠A+2∠1),
(∠A+2∠1),
即2∠D=360°-2∠3-∠A-2∠1=360°-2(∠1+∠3)-∠A----②,
把①代入②得2∠D=∠A.
分析:(1)根据三角形角平分线的性质可得,∠BOC+∠OCB=90°- ∠A,根据三角形内角和定理可得∠BOC=90°+
∠A,根据三角形内角和定理可得∠BOC=90°+ ∠A;
∠A;
(2)根据三角形外角平分线的性质可得∠BCD= (∠A+∠ABC)、∠DBC=
(∠A+∠ABC)、∠DBC= (∠A+∠ACB);根据三角形内角和定理可得∠BDC=90°-
(∠A+∠ACB);根据三角形内角和定理可得∠BDC=90°- ∠A;
∠A;
(3)根据BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,可知,∠A=180°-∠1-∠3,∠D=180°-∠4=∠5=180°-∠3- (∠A+2∠1),两式联立可得2∠D=∠A.
(∠A+2∠1),两式联立可得2∠D=∠A.
点评:此类题目比较简单,考查的是三角形内角与外角的关系,角平分线的性质,三角形内角和定理,属中学阶段的常规题.
∴∠OBC+∠OCB=
 (180°-∠A)=
(180°-∠A)= ×(180°-x°)=90°-
×(180°-x°)=90°- ∠A
∠A故∠BOC=180°-(∠OBC+∠OCB)=180°-(90°-
 ∠A)=90°+
∠A)=90°+ ∠A;
∠A;(2)∵BD、CD为△ABC两外角∠ABC、∠ACB的平分线,∠A为x°
∴∠BCD=
 (∠A+∠ABC)、∠DBC=
(∠A+∠ABC)、∠DBC= (∠A+∠ACB),
(∠A+∠ACB),由三角形内角和定理得,∠BDC=180°-∠BCD-∠DBC,
=180°-
 [∠A+(∠A+∠ABC+∠ACB)],
[∠A+(∠A+∠ABC+∠ACB)],=180°-
 (∠A+180°),
(∠A+180°),=90°-
 ∠A;
∠A;(3)如图:∵BD为△ABC的角平分线,交AC与点E,CD为△ABC外角∠ACE的平分线,两角平分线交于点D
∴∠1=∠2,∠5=
 (∠A+2∠1),∠3=∠4,
(∠A+2∠1),∠3=∠4,在△ABE中,∠A=180°-∠1-∠3
∴∠1+∠3=180°-∠A----①
在△CDE中,∠D=180°-∠4-∠5=180°-∠3-
 (∠A+2∠1),
(∠A+2∠1),即2∠D=360°-2∠3-∠A-2∠1=360°-2(∠1+∠3)-∠A----②,
把①代入②得2∠D=∠A.

分析:(1)根据三角形角平分线的性质可得,∠BOC+∠OCB=90°-
 ∠A,根据三角形内角和定理可得∠BOC=90°+
∠A,根据三角形内角和定理可得∠BOC=90°+ ∠A;
∠A;(2)根据三角形外角平分线的性质可得∠BCD=
 (∠A+∠ABC)、∠DBC=
(∠A+∠ABC)、∠DBC= (∠A+∠ACB);根据三角形内角和定理可得∠BDC=90°-
(∠A+∠ACB);根据三角形内角和定理可得∠BDC=90°- ∠A;
∠A;(3)根据BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,可知,∠A=180°-∠1-∠3,∠D=180°-∠4=∠5=180°-∠3-
 (∠A+2∠1),两式联立可得2∠D=∠A.
(∠A+2∠1),两式联立可得2∠D=∠A.点评:此类题目比较简单,考查的是三角形内角与外角的关系,角平分线的性质,三角形内角和定理,属中学阶段的常规题.

练习册系列答案
相关题目
 52、如图所示,已知AB=AC,EB=EC,AE的延长线交BC于D,那么图中的全等三角形共有
52、如图所示,已知AB=AC,EB=EC,AE的延长线交BC于D,那么图中的全等三角形共有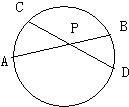 9、如图所示,已知⊙O中,弦AB,CD相交于点P,AP=6,BP=2,CP=4,则PD的长是( )
9、如图所示,已知⊙O中,弦AB,CD相交于点P,AP=6,BP=2,CP=4,则PD的长是( ) 如图所示,已知等边△ABC的两个顶点的坐标为A(-4,0),B(2,0).
如图所示,已知等边△ABC的两个顶点的坐标为A(-4,0),B(2,0).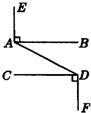 24、如图所示,已知EA⊥AB于点A,CD⊥DF于点D,AB∥CD,请判断EA与DF的位置关系,并说明理由.
24、如图所示,已知EA⊥AB于点A,CD⊥DF于点D,AB∥CD,请判断EA与DF的位置关系,并说明理由. 如图所示,已知等边△ABC的边长为a,P是△ABC内一点,PD∥AB,PE∥BC,PF∥AC,点D、E、F分别在BC、AC、AB上,猜想:PD+PE+PF=
如图所示,已知等边△ABC的边长为a,P是△ABC内一点,PD∥AB,PE∥BC,PF∥AC,点D、E、F分别在BC、AC、AB上,猜想:PD+PE+PF=