题目内容
 如图所示,已知等边△ABC的两个顶点的坐标为A(-4,0),B(2,0).
如图所示,已知等边△ABC的两个顶点的坐标为A(-4,0),B(2,0).试求:
(1)C点的坐标;
(2)△ABC的面积.
分析:(1)作CH⊥AB于H.根据点A和B的坐标,得AB=6.根据等腰三角形的三线合一的性质,得AH=BH=3,再根据勾股定理求得CH=3
,从而写出点C的坐标;
(2)根据三角形的面积公式进行计算.
| 3 |
(2)根据三角形的面积公式进行计算.
解答: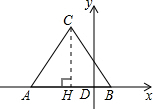 解:(1)作CH⊥AB于H.
解:(1)作CH⊥AB于H.
∵A(-4,0),B(2,0),
∴AB=6.
∵△ABC是等边三角形,
∴AH=BH=3.
根据勾股定理,得CH=3
.
∴C(-1,3
);
同理,当点C在第三象限时,C(-1,-3
).
故C点坐标为:C(-1,3
)或(-1,-3
);
(2)S△ABC=
×6×3
=9
.
 解:(1)作CH⊥AB于H.
解:(1)作CH⊥AB于H.∵A(-4,0),B(2,0),
∴AB=6.
∵△ABC是等边三角形,
∴AH=BH=3.
根据勾股定理,得CH=3
| 3 |
∴C(-1,3
| 3 |
同理,当点C在第三象限时,C(-1,-3
| 3 |
故C点坐标为:C(-1,3
| 3 |
| 3 |
(2)S△ABC=
| 1 |
| 2 |
| 3 |
| 3 |
点评:此题综合运用了等边三角形的性质和勾股定理,熟练运用三角形的面积公式.x轴上两点间的距离等于两点的横坐标的差的绝对值.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目


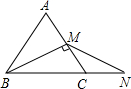 如图所示,已知等边三角形ABC的周长是2a,BM是AC边上的高,N为BC延长线上的一点,且CN=CM,则BN=
如图所示,已知等边三角形ABC的周长是2a,BM是AC边上的高,N为BC延长线上的一点,且CN=CM,则BN=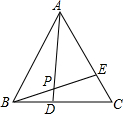 如图所示,已知等边△ABC中,BD=CE,AD与BE相交于点P,求∠APE是度数.
如图所示,已知等边△ABC中,BD=CE,AD与BE相交于点P,求∠APE是度数.