题目内容
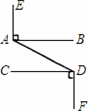
 24、如图所示,已知EA⊥AB于点A,CD⊥DF于点D,AB∥CD,请判断EA与DF的位置关系,并说明理由.
24、如图所示,已知EA⊥AB于点A,CD⊥DF于点D,AB∥CD,请判断EA与DF的位置关系,并说明理由.分析:首先由AB∥CD,根据两直线平行,内错角相等,得到∠BAD=∠ADC,再根据垂直的定义得到∠EAB=∠CDF=90°,则∠EAB+∠BAD=∠CDF+∠ADC,即∠EAD=∠ADF,满足关于EA∥DF的条件:内错角相等,两直线平行.
解答:解:EA∥DF.
理由如下:
∵EA⊥AB于点A,CD⊥DF于点D(已知),
∴∠EAB=90°,∠CDF=90°(垂直定义).
∵AB∥CD(已知),
∴∠BAD=∠ADC(两直线平行,内错角相等),
∴∠EAB+∠BAD=∠CDF+∠ADC,即∠EAD=∠ADF,
∴EA∥DF(内错角相等,两直线平行).
理由如下:
∵EA⊥AB于点A,CD⊥DF于点D(已知),
∴∠EAB=90°,∠CDF=90°(垂直定义).
∵AB∥CD(已知),
∴∠BAD=∠ADC(两直线平行,内错角相等),
∴∠EAB+∠BAD=∠CDF+∠ADC,即∠EAD=∠ADF,
∴EA∥DF(内错角相等,两直线平行).
点评:本题考查了平行线的性质,垂直的定义以及平行线的判定定理.

练习册系列答案
相关题目
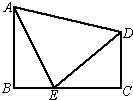 6、如图所示,已知在直角梯形ABCD中,∠B=∠C=90°,E为BC上的点,且EA=ED,∠AEB=75°,∠DEC=45°,试说明AB=BC.
6、如图所示,已知在直角梯形ABCD中,∠B=∠C=90°,E为BC上的点,且EA=ED,∠AEB=75°,∠DEC=45°,试说明AB=BC.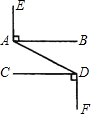 如图所示,已知EA⊥AB于点A,CD⊥DF于点D,AB∥CD,请判断EA与DF的位置关系,并说明理由.
如图所示,已知EA⊥AB于点A,CD⊥DF于点D,AB∥CD,请判断EA与DF的位置关系,并说明理由.