题目内容
将一元二次方程x2-2x-4=0用配方法化成(x-a)2=b的形式为 ,则方程的根为 .
考点:解一元二次方程-配方法
专题:计算题
分析:方程常数项移到右边,两边加上1变形后,利用完全平方公式化简,开方即可求出解.
解答:解:方程x2-2x-4=0,
移项得:x2-2x=4,
配方得:x2-2x+1=5,即(x-1)2=5,
开方得:x-1=±
,
解得:x1=1+
,x2=1-
.
故答案为:(x-1)2=5;x1=1+
,x2=1-
移项得:x2-2x=4,
配方得:x2-2x+1=5,即(x-1)2=5,
开方得:x-1=±
| 5 |
解得:x1=1+
| 5 |
| 5 |
故答案为:(x-1)2=5;x1=1+
| 5 |
| 5 |
点评:此题考查了解一元二次方程-配方法,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知m、n是两个连续自然数(m<n),且q=mn,设p=
+
,则p( )
| q+n |
| q-n |
| A、总是奇数 |
| B、总是偶数 |
| C、有时是奇数,有时是偶数 |
| D、有时是有理数,有时是无理数 |
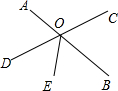 如图,∠DOE的邻补角是
如图,∠DOE的邻补角是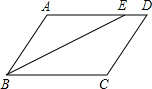 如图,?ABCD中,BE平分∠ABC且交边AD于点E,如果AB=6cm,BC=10cm,则线段DE=
如图,?ABCD中,BE平分∠ABC且交边AD于点E,如果AB=6cm,BC=10cm,则线段DE=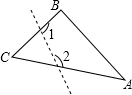 如图,△ABC中,∠C=50°,若沿图中虚线剪去∠C,则∠1+∠2=
如图,△ABC中,∠C=50°,若沿图中虚线剪去∠C,则∠1+∠2=