题目内容
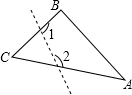如图，△ABC中，∠C=50°，若沿图中虚线剪去∠C，则∠1+∠2=考点：多边形内角与外角,三角形内角和定理
专题：
分析：首先根据三角形内角和可以计算出∠A+∠B的度数，再根据四边形内角和为360°可算出∠1+∠2的结果．
解答：解：∵△ABC中，∠C=50°，
∴∠A+∠B=180°-∠C=130°，
∵∠A+∠B+∠1+∠2=360°，
∴∠1+∠2=360°-130°=230°．
故答案为：230．
∴∠A+∠B=180°-∠C=130°，
∵∠A+∠B+∠1+∠2=360°，
∴∠1+∠2=360°-130°=230°．
故答案为：230．
点评：此题主要考查了三角形内角和以及多边形内角和，关键是掌握多边形内角和定理：（n-2）．180° （n≥3）且n为整数）．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
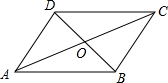如图，在平行四边形ABCD中，对角线AC、BD交于点O，AC=10cm，BD=8cm，边AB=6cm，则△DOC的周长为
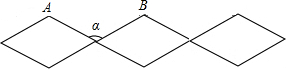如图是根据四边形的不稳定性制作的可活动的衣架，图中每个菱形的边长为16cm，若墙上相邻的两个钉子AB之间的距离为下列选项中正确的是（ ）
A、
| ||||
B、(-
| ||||
C、(x-
| ||||
| D、平行四边形的对角线相等 |