题目内容
如图,在半径为6,圆心角为90°的扇形OAB的 | AB |
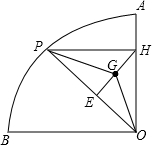
(1)设PH=x,S△PGH=y,求y关于x的函数解析式;
(2)△PGH的面积是否有最大值?如果有,求出最大面积,并求出此时PH的长度;如果没有,请说明理由;
(3)如果△PGH为等腰三角形,试求出线段PH的长.
分析:(1)本题的关键是要掌握三角形重心的概念,三角形重心是三角形三条中线的交点,且重心到顶点的距离与重心到对边中点的距离之比为2:1;结合等高三角形的面积比等于底边的比,可得出S△PGH=
S△POH=
S△POH,因此只需求出三角形POH的面积即可.
(2)根据(1)得出的函数的性质可求得S的最大值.
(3)本题要分三种情况:
①PG=GH,此时PD=HE,三角形PDO和OEH全等,OP=OH,此时P、H、A重合,因此PH=0,显然不合题意.
②PG=PH,PG=PH=x,PD=
x,可在直角三角形PHD中,用勾股定理求出x的值.
③PH=GH,由于HE是直角三角形斜边上的中线,因此HE=
OP=3,因此HG=PH=2.
| 2 |
| 3 |
| 1 |
| 3 |
(2)根据(1)得出的函数的性质可求得S的最大值.
(3)本题要分三种情况:
①PG=GH,此时PD=HE,三角形PDO和OEH全等,OP=OH,此时P、H、A重合,因此PH=0,显然不合题意.
②PG=PH,PG=PH=x,PD=
| 2 |
| 3 |
③PH=GH,由于HE是直角三角形斜边上的中线,因此HE=
| 1 |
| 2 |
解答:解:(1)延长PG交OH于点D,
∵PG:GD=2:1,
∴S△PGH=
S△POH=
S△POH
由勾股定理得OH=
=
∴y=
×
PH•OH=
x
(0<x<6);
(2)∵y2=
x2(36-x2)(0<x<6),
令t=x2,则y2=
t(36-t)=-
t2+t(0<t<36),是关于t的二次函数,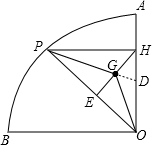
当t=18时,y2取最小值为9,
此时y=3,x=3
,即当PH=3
时,△PGH有大面积3;
(3)延长HG交OP于点E,则HE=
OP=3,
∴HG=
HE=2,
又∵DH=
OH=
,
∴DP=
=
=
,
∴PH=
DP=
(0<x<6),△PGH为等腰三角形,有三种可能情况:
1、GP=PH,即
=x解得x=
;
2、GP=GH,即
=2解得x=0,不合;
3、PH=GH,即x=2
综上,若PH为2或
时,△PGH为等腰三角形.
∵PG:GD=2:1,
∴S△PGH=
| 2 |
| 3 |
| 1 |
| 3 |
由勾股定理得OH=
| OP2-PH2 |
| 36-x2 |
∴y=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 36-x2 |
(2)∵y2=
| 1 |
| 36 |
令t=x2,则y2=
| 1 |
| 36 |
| 1 |
| 36 |

当t=18时,y2取最小值为9,
此时y=3,x=3
| 2 |
| 2 |
(3)延长HG交OP于点E,则HE=
| 1 |
| 2 |
∴HG=
| 2 |
| 3 |
又∵DH=
| 1 |
| 2 |
| 1 |
| 2 |
| 36-x2 |
∴DP=
| DH2+PH2 |
|
| 1 |
| 2 |
| 36+3x2 |
∴PH=
| 2 |
| 3 |
| 1 |
| 3 |
| 36+3x2 |
1、GP=PH,即
| 1 |
| 3 |
| 36+3x2 |
| 6 |
2、GP=GH,即
| 1 |
| 3 |
| 36+3x2 |
3、PH=GH,即x=2
综上,若PH为2或
| 6 |
点评:本题主要考查了三角形、圆和二次函数的相关知识,(1)题弄清三角形重心的定义和性质是解题的关键,(3)在不确定等腰三角形的腰和底的情况下要分类求解.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
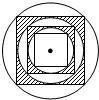 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
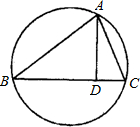 如图,在半径为R的圆中作一内接△ABC,使BC边上的高AD=h(定值),这样的三角形可作出无数个,但AB•AC为定值,其值为
如图,在半径为R的圆中作一内接△ABC,使BC边上的高AD=h(定值),这样的三角形可作出无数个,但AB•AC为定值,其值为 8、如图:在半径为1的圆中,弦CD垂直平分AB,则CD=
8、如图:在半径为1的圆中,弦CD垂直平分AB,则CD= 如图,在半径为6cm的圆中,弦AB长6
如图,在半径为6cm的圆中,弦AB长6 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是