题目内容
 如图,在半径为6cm的圆中,弦AB长6
如图,在半径为6cm的圆中,弦AB长6| 3 |
分析:设弦AB在优弧上所对的圆周角为∠P,劣弧上所对的圆周角为∠P′,连接OA,OB,过O点作OC⊥AB,垂足为C,由垂径定理可知AC=
AB=3
,解直角三角形得∠AOC的度数,由垂径定理可知,∠AOB=2∠AOC,由圆周角定理得∠P=
∠AOB,利用∠P与∠P′的互余关系求∠P′.
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
解答: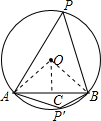 解:如图,设弦AB在优弧上所对的圆周角为∠P,劣弧上所对的圆周角为∠P′,
解:如图,设弦AB在优弧上所对的圆周角为∠P,劣弧上所对的圆周角为∠P′,
连接OA,OB,过O点作OC⊥AB,垂足为C,
由垂径定理,得AC=
AB=3
,
在Rt△AOC中,OA=6,sin∠AOC=
=
=
,
解得∠AOC=60°,
所以,∠AOB=2∠AOC=120°,
根据圆周角定理,得∠P=
∠AOB=60°,
又APBP′为圆内接四边形,
所以,∠P′=180°-∠P=120°,
故弦AB所对的圆周角的度数为60°或120°
 解:如图,设弦AB在优弧上所对的圆周角为∠P,劣弧上所对的圆周角为∠P′,
解:如图,设弦AB在优弧上所对的圆周角为∠P,劣弧上所对的圆周角为∠P′,连接OA,OB,过O点作OC⊥AB,垂足为C,
由垂径定理,得AC=
| 1 |
| 2 |
| 3 |
在Rt△AOC中,OA=6,sin∠AOC=
| AC |
| OA |
3
| ||
| 6 |
| ||
| 2 |
解得∠AOC=60°,
所以,∠AOB=2∠AOC=120°,
根据圆周角定理,得∠P=
| 1 |
| 2 |
又APBP′为圆内接四边形,
所以,∠P′=180°-∠P=120°,
故弦AB所对的圆周角的度数为60°或120°
点评:本题考查了垂径定理,解直角三角形的运用.关键是连接半径,将问题转化到直角三角形中,解直角三角形求圆心角,再求圆周角,注意弦所对的圆周角有两个,它们互补.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
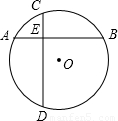
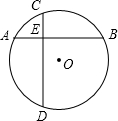 如图,在半径为6cm的⊙O中,弦AB⊥CD,垂足为E,若CE=3cm,DE=7cm,则AB=
如图,在半径为6cm的⊙O中,弦AB⊥CD,垂足为E,若CE=3cm,DE=7cm,则AB= cm,试求弦AB所对的圆周角的度数.
cm,试求弦AB所对的圆周角的度数.