题目内容
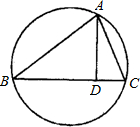 如图,在半径为R的圆中作一内接△ABC,使BC边上的高AD=h(定值),这样的三角形可作出无数个,但AB•AC为定值,其值为
如图,在半径为R的圆中作一内接△ABC,使BC边上的高AD=h(定值),这样的三角形可作出无数个,但AB•AC为定值,其值为分析:因为题目要求中的高AD=h是个定值,那么我们要求的AB.AC的值就用圆的半径R和高h表示出来即可,题目涉及了半径,我们就可以考虑到作圆的直径,制造直角三角形与题目中已知的直角三角形ADC或ABD相似,就可以使问题得到解决.
解答: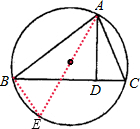 解:作⊙O的直径交⊙O于点E,连接BE,
解:作⊙O的直径交⊙O于点E,连接BE,
∴∠ABE=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠ABE=∠ADC,
∵∠E=∠C,
∴△ABE∽△ADC,
∴
=
,
即AB.AC=AD.AE,
∵AE=2R,AD=h,
∴AB.AC=2Rh,
故答案为:2Rh.
 解:作⊙O的直径交⊙O于点E,连接BE,
解:作⊙O的直径交⊙O于点E,连接BE,∴∠ABE=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠ABE=∠ADC,
∵∠E=∠C,
∴△ABE∽△ADC,
∴
| AB |
| AD |
| AE |
| AC |
即AB.AC=AD.AE,
∵AE=2R,AD=h,
∴AB.AC=2Rh,
故答案为:2Rh.
点评:本题考查了相似三角形的判定与性质,圆周角定理的运用,运用了直径所对的圆周角为直角这个特殊的性质.

练习册系列答案
相关题目
 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
 如图,在半径为6cm的圆中,弦AB长6
如图,在半径为6cm的圆中,弦AB长6 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是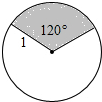 如图,在半径为1的圆中,圆心角为120°的扇形AOB的面积等于
如图,在半径为1的圆中,圆心角为120°的扇形AOB的面积等于