题目内容
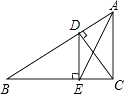
【题目】如图，在△ABC中，∠BAC=90°，AB=AC=3，点D在BC上且BD=2CD，E，F分别在AB，AC上运动且始终保持∠EDF=45°，设BE=x，CF=y，则y与x之间的函数关系用图象表示为：（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】试题分析：根据等边对等角可得∠B=∠C=45°，且根据勾股定理可求得BC=
，然后可根据
三角形的内角和可知∠BDE+∠BED=180°-∠B=135°，由∠EDF=45°，可知∠BDE+∠CDF=180°-∠EDF=135°，因此可得∠BDE=∠CDF，由两角对应相等的两三角形相似可得△BED∽△CDF，然后根据相似三角形的性质可得
，再由BD=2CD可得BD=
，CD=
，即
，解得
，然后根据E，F分别在AB，AC上运动，可得0＜x≤3，0＜y≤3，可知D正确.
故选：D.
练习册系列答案
阅读快车系列答案
相关题目
