题目内容
【题目】如图,在平面直角坐标系中,一次函数的图象y1=kx+b与反比例函数![]() 的图象交于点A(1,5)和点B(m,1).
的图象交于点A(1,5)和点B(m,1).
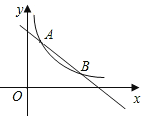
(1)求m的值和反比例函数的解析式;
(2)当x>0时,根据图象直接写出不等式![]() ≥kx+b的解集;
≥kx+b的解集;
(3)若经过点B的抛物线的顶点为A,求该抛物线的解析式.
【答案】(1)m的值为5,比例函数的解析式为![]() ;
;
(2)不等式![]() ≥kx+b的解集为0<x≤1或x≥5;
≥kx+b的解集为0<x≤1或x≥5;
(3)该抛物线的解析式是![]() .
.
【解析】试题分析:(1)把点A(1,5)代入y2=![]() ,求得n=5,再把 B(m,1)代入y2=
,求得n=5,再把 B(m,1)代入y2=![]() 得m=5,
得m=5,
再把A(1,5)、B(5,1)代入y1=kx+b, 即可得解;
(2)根据函数图象及交点坐标即可求解;
(3)设二次函数的解析式为设抛物线的解析式为![]() ,把B(5,1)代入解析式即可得解.
,把B(5,1)代入解析式即可得解.
试题解析:(1)∵反比例函数![]() 的图象交于点A(1,5),
的图象交于点A(1,5),
∴5=n,即n=5,
∴y2=![]() ,
,
∵点B(m,1)在双曲线上.
∴1=![]() ,
,
∴m=5,
∴B(5,1);
(2)不等式![]() ≥kx+b的解集为0<x≤1或x≥5;
≥kx+b的解集为0<x≤1或x≥5;
(3)∵抛物线的顶点为A(1,5),
∴设抛物线的解析式为![]() ,
,
∵抛物线经过B(5,1),
∴![]() ,解得
,解得![]() .
.
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目