题目内容
如图,在直角坐标系中,A(-1,0),B(0,2),一动点P沿过B点且垂直于AB的射线BM运动,P点的运动速度为每秒1个单位长度,射线BM与x轴交于点C.
(1)求点C的坐标.
(2)求过点A、B、C三点的抛物线的解析式.
(3)若P点开始运动时,Q点也同时从C点出发,以P点相同的速度沿x轴负方向向点A运动,t秒后,以P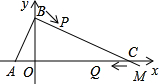 、Q、C为顶点的三角形是等腰三角形.(点P到点C时停止运动,点Q也同时停止运动),求t的值.
、Q、C为顶点的三角形是等腰三角形.(点P到点C时停止运动,点Q也同时停止运动),求t的值.
(4)在(2)(3)的条件下,当CQ=CP时,求直线OP与抛物线的交点坐标.
(1)求点C的坐标.
(2)求过点A、B、C三点的抛物线的解析式.
(3)若P点开始运动时,Q点也同时从C点出发,以P点相同的速度沿x轴负方向向点A运动,t秒后,以P
 、Q、C为顶点的三角形是等腰三角形.(点P到点C时停止运动,点Q也同时停止运动),求t的值.
、Q、C为顶点的三角形是等腰三角形.(点P到点C时停止运动,点Q也同时停止运动),求t的值.(4)在(2)(3)的条件下,当CQ=CP时,求直线OP与抛物线的交点坐标.
(1)∵A(-1,0),B(0,2),
∴OA=1,OB=2,OB=2OA;
∵∠ABC=90°,易得△ABO∽△BCO,
∴AO:BO=BO:OC,即OC=2OB=4,
∴C(4,0).
(2)设抛物线方程为y=ax2+bx+c(a≠0),依题意有:
,
解得
;
∴抛物线的解析式为y=-
x2+
x+2.
(3)∵OB=2,OC=4,
∴BC=2
;
则:BP=t,CP=2
-t,CQ=t;
①CP=CQ,则有:2
-t=t,
解得:t=
;
②CQ=QP,过Q作QM′⊥BC于M′,则有:
CM′=
(2
-t);
易证△CQM′∽△CBO,
则:
=
,
即
=
,
解得:t=
=
;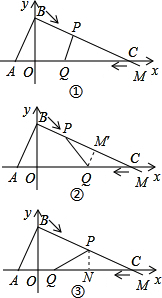
③CP=PQ,过P作PN⊥OC于N,则:
CN=
CQ=
t;
易证△CNP∽△COB,则有:
=
,
即
=
,
解得t=
=
;
综上所述,当t=
或
或
时,以P、Q、C为顶点的三角形是等腰三角形.
(4)由(3)知:当CP=CQ时,BP=t=
=
BC,即P是BC的中点,
∵B(0,2),C(4,0),
∴P(2,1);
∴直线OP的解析式为:y=
x;
联立抛物线的解析式有:
,
解得
,
;
∴直线OP与抛物线的交点为(1+
,
),(1-
,
).
∴OA=1,OB=2,OB=2OA;
∵∠ABC=90°,易得△ABO∽△BCO,
∴AO:BO=BO:OC,即OC=2OB=4,
∴C(4,0).
(2)设抛物线方程为y=ax2+bx+c(a≠0),依题意有:
|
解得
|
∴抛物线的解析式为y=-
| 1 |
| 2 |
| 3 |
| 2 |
(3)∵OB=2,OC=4,
∴BC=2
| 5 |
则:BP=t,CP=2
| 5 |
①CP=CQ,则有:2
| 5 |
解得:t=
| 5 |
②CQ=QP,过Q作QM′⊥BC于M′,则有:
CM′=
| 1 |
| 2 |
| 5 |
易证△CQM′∽△CBO,
则:
| CQ |
| CB |
| CM′ |
| OC |
即
| t | ||
2
|
| ||||
| 4 |
解得:t=
| 10 | ||
4+
|
40-10
| ||
| 11 |

③CP=PQ,过P作PN⊥OC于N,则:
CN=
| 1 |
| 2 |
| 1 |
| 2 |
易证△CNP∽△COB,则有:
| CN |
| OC |
| CP |
| CB |
即
| ||
| 4 |
2
| ||
2
|
解得t=
8
| ||
4+
|
32
| ||
| 11 |
综上所述,当t=
| 5 |
40-10
| ||
| 11 |
32
| ||
| 11 |
(4)由(3)知:当CP=CQ时,BP=t=
| 5 |
| 1 |
| 2 |
∵B(0,2),C(4,0),
∴P(2,1);
∴直线OP的解析式为:y=
| 1 |
| 2 |
联立抛物线的解析式有:
|
解得
|
|
∴直线OP与抛物线的交点为(1+
| 5 |
1+
| ||
| 2 |
| 5 |
1-
| ||
| 2 |

练习册系列答案
相关题目




 标,画出满足条件的P点,并求出经过D、P、C三点的抛物线的对称轴;若不存在这样的P点,请说明理由.
标,画出满足条件的P点,并求出经过D、P、C三点的抛物线的对称轴;若不存在这样的P点,请说明理由.
 不存在,请说明理由!
不存在,请说明理由!