��Ŀ����
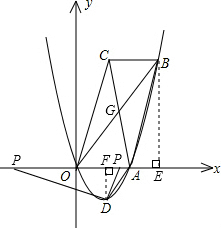
��ͼ����ƽ��ֱ������ϵ�У�OΪԭ�㣬��֪A��2��0����C��1��3
��������OAC��AC���е�G��ת180�㣬��O�䵽��B��λ�ã�������y=ax2-2
x������A����D�������ߵĶ��㣮
��1���������ߵı���ʽ��
��2���жϵ�B�Ƿ����������ϣ�
��3������P��x����A����ߵ�һ�����㣬����P��A��DΪ��������������OAB����ʱ�������P�����ꣻ
��4������M��y���ϵ�һ�����㣬Ҫʹ��MAD���ܳ���С����ֱ��д����M�����꣮

| 3 |
| 3 |
��1���������ߵı���ʽ��
��2���жϵ�B�Ƿ����������ϣ�
��3������P��x����A����ߵ�һ�����㣬����P��A��DΪ��������������OAB����ʱ�������P�����ꣻ
��4������M��y���ϵ�һ�����㣬Ҫʹ��MAD���ܳ���С����ֱ��д����M�����꣮

��1����A��2��0������y=ax2-2
x�ã�
4a-4
=0��
���a=
��
�������ߵĽ���ʽΪy=
x2-2
x��
��2������ת֪���ı���OABC��ƽ���ı��Σ�
��BC��OA��BC=AO��
��A��2��0����C��1��3
����
��xB=1+2=3��yB=yC=3
��
��B��3��3
����
��B��3��3
������y=
x2-2
x�ã�
��32-2
��3=3
��
���B���������ϣ�
��3������B��BE��x����E������D��DF��x����F��
��y=
x2-2
x=
��x-1��2-
�ö���D��1��-
����
��B��3��3
����
����Rt��BOE��Rt��DAF��tan��BOE=
=
=
��
tan��DAF=
=
=
��
���BOE=��DAF=60�㣬
��OA=2��OB=
=6��
AD=
=2��
���APD�͡�OAB���Ʒ��������������
��APD=��OABʱ��APD�͡�OAB���ƣ�
��
=
��
��
=
��
���AP=
��
��OP=OA-AP=2-
=
��
���P��������
��0����
�ڡ�APD=��OBAʱ��APD�͡�OBA���ƣ�
��
=
��
��
=
��
���AP=6��
��OP=AP-OA=6-2=4��
���P��������-4��0����
������������P��
��0����-4��0����
��4����A��2��0������y��ĶԳƵ�A������Ϊ��-2��0����
������Գ�ȷ�����·�ߣ�ֱ��A��D��y��Ľ��㼴Ϊʹ��MAD���ܳ���С�ĵ�M��λ�ã�
��ֱ��A��D�Ľ���ʽΪy=kx+b��
��
��
���
��
��ֱ��A��D�Ľ���ʽΪy=-
x-
��
x=0ʱ��y=-
��
���M��������0��-
����
| 3 |
4a-4
| 3 |
���a=
| 3 |
�������ߵĽ���ʽΪy=
| 3 |
| 3 |
��2������ת֪���ı���OABC��ƽ���ı��Σ�
��BC��OA��BC=AO��
��A��2��0����C��1��3
| 3 |
��xB=1+2=3��yB=yC=3
| 3 |
��B��3��3
| 3 |
��B��3��3
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
���B���������ϣ�
��3������B��BE��x����E������D��DF��x����F��
��y=
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
��B��3��3
| 3 |
����Rt��BOE��Rt��DAF��tan��BOE=
| BE |
| OE |
3
| ||
| 3 |
| 3 |
tan��DAF=
| DF |
| AF |
| ||
| 2-1 |
| 3 |
���BOE=��DAF=60�㣬
��OA=2��OB=
32+(3
|
AD=
(2-1)2+(
|
���APD�͡�OAB���Ʒ��������������
��APD=��OABʱ��APD�͡�OAB���ƣ�
��
| AP |
| OA |
| AD |
| OB |
��
| AP |
| 2 |
| 2 |
| 6 |
���AP=
| 2 |
| 3 |
��OP=OA-AP=2-
| 2 |
| 3 |
| 4 |
| 3 |
���P��������
| 4 |
| 3 |
�ڡ�APD=��OBAʱ��APD�͡�OBA���ƣ�
��
| AP |
| OB |
| AD |
| OA |

��
| AP |
| 6 |
| 2 |
| 2 |
���AP=6��
��OP=AP-OA=6-2=4��
���P��������-4��0����
������������P��
| 4 |
| 3 |
��4����A��2��0������y��ĶԳƵ�A������Ϊ��-2��0����
������Գ�ȷ�����·�ߣ�ֱ��A��D��y��Ľ��㼴Ϊʹ��MAD���ܳ���С�ĵ�M��λ�ã�
��ֱ��A��D�Ľ���ʽΪy=kx+b��
��
|
���
|
��ֱ��A��D�Ľ���ʽΪy=-
| ||
| 3 |
2
| ||
| 3 |
x=0ʱ��y=-
2
| ||
| 3 |
���M��������0��-
2
| ||
| 3 |

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
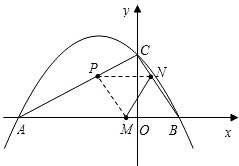 BC��B��C���������ֱ�ΪB��1��0����
BC��B��C���������ֱ�ΪB��1��0����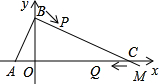 ��Q��CΪ������������ǵ��������Σ�����P����Cʱֹͣ�˶�����QҲͬʱֹͣ�˶�������t��ֵ��
��Q��CΪ������������ǵ��������Σ�����P����Cʱֹͣ�˶�����QҲͬʱֹͣ�˶�������t��ֵ��