题目内容
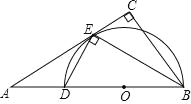
【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
①∠AOB=90°+![]() ∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )
∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )

A. ①② B. ③④ C. ①②④ D. ①③④
【答案】C
【解析】因为∠BAC和∠ABC的平分线相交于点O,所以∠OBA=![]() ∠CBA, ∠OAB=
∠CBA, ∠OAB=![]() ∠CAB,所以∠AOB=
∠CAB,所以∠AOB=![]() ∠CBA-
∠CBA-![]() ∠CAB=
∠CAB=![]() =90°+
=90°+ ![]() , ①正确,
, ①正确,
因为EF∥AB,所以∠FOB=∠ABO,又∠ABO=∠FBO,所以∠FOB=∠FBO,所以FO=FB,
同理EO=EA,所以AE+BF=EF, ②正确,
当∠C=![]() 时,AE+BF=EF<CF+CE,所以E,F分别是AC,BC的中点, ③错误,
时,AE+BF=EF<CF+CE,所以E,F分别是AC,BC的中点, ③错误,
作OH⊥AC于H,
因为∠BAC和∠ABC的平分线相交于点O,所以点O在∠C的平分线上,
所以OD=OH,所以S△CEF= ![]() , ④正确,
, ④正确,
故选C.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目