题目内容
【题目】定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的“三阶等腰线”.
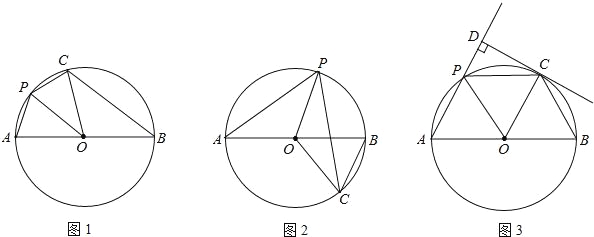
(1)请你在图1,图2中用两种不同的方法画出顶角为36°的等腰三角形的“三阶等腰线”,并标注每个等腰三角形顶角的度数.(若两种方法分得的三角形成3对全等三角形,则视为同一种).
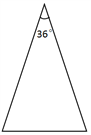



图1 图2 备用1 备用2
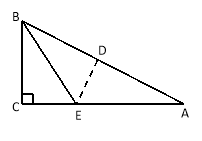
(2)△ABC中,∠B=36°,AD和DE是△ABC的“三阶等腰线”,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值.
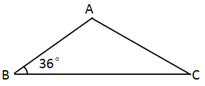
【答案】(1)画图见解析;(2)满足条件的x=24或 36.
【解析】试题分析:(1)根据等腰三角形的性质和三阶等腰线的定义: ①可以作两底角角平分线, ②先作底角角平分线,再作平行线,
(2)先根据三角形内角和,等腰三角形的性质和三阶等腰线的定义,画满足要求的图形,然后根据等腰三角形的性质用x表示出三角形的内角,利用三角形内角和列出关于x的方程,解方程即可.
试题解析:(1)如图所示:
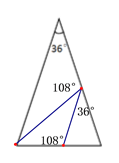
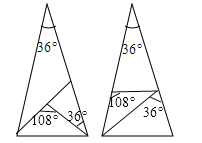
(2)①当AD=AE时,
∵2x+x=36+36,
∴x=24.
②当AD=DE时,
∵36+36+2x+x=180,
∴x=36.
③当EA=DE时,
∵90- x+36+36+x=180,
∴x不存在,应舍去.
综合上述:满足条件的x=24或 36.


练习册系列答案
相关题目